A lodestone is a naturally occuring piece of magnetic material. It exhibits ferromagnetism. There are actually three (3) types of magnetism:
- Ferromagnetism
- Paramagnetism
- Diamagnetism
Bar magnets, which are typically made of an alloy of iron, show two types of magnetic poles (magnetic north and south). These poles repel or attract each other based on their polarity.
The Law of Magnetism
This states that like poles repel and unlike poles attract. It implies:
- north-north repulsion
- south-south repulsion
- north-south attraction
Magnetic fields
A magnetic field is the region in space around a magnetic field, within which a magnetic force (be it attractive or repulsive) is experienced.
Field lines
These are the lines we use to represent the magnetic field. The number of these lines passing through a cross-section of a surface is used to indicate the strength of the field passing through that surface. For example, we draw the field lines at the poles of a bar magnet very close together but the lines around the sides of the magnet as being far apart.
Image Credits: HyperPhysics
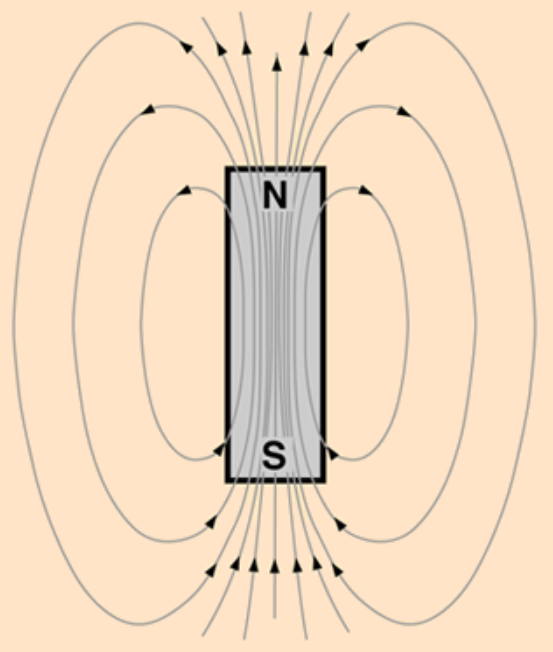
This is a way for us to indicate that the magnetic force that is exerted close to the poles of the magnet is much stronger than that at the sides of the magnet.
The Magnetic North and South poles of the Earth aren’t always the same as True North and South. There is a dip angle between the true axis of the Earth and its magnetic axis. As we track the direction of the magnetic field at different parts on the Earth’s surface, we will see that the direction of the field changes and thus what apppears to be north also changes.
The direction of the field
In the same way we define the direction of an electric field as the direction in which a positive point charge would move:
The direction of the magnetic field at a point is the direction in which a north pole would move when placed at that point.
Magnetic flux density
This is the force acting per unit current per unit length on a wire placed perpendicular to a magnetic field: $$ \begin{equation}\begin{aligned} B=\frac{F}{Il}\\ \end{aligned}\end{equation} $$
Being a force, it is a vector quantity and has an SI unit of the Tesla($T$): $$ \begin{equation}\begin{aligned} B=\frac{F}{Il}\rightarrow \frac{N}{A\times m}=T\\ \end{aligned}\end{equation} $$
The flux density is comparable to the number of lines passing through a cross section of the surface.
Force on a current carrying conductor
The force, $F$, on a wire placed in between two unlike poles can be determined using the formula:
$$ \begin{equation}\begin{aligned} F=BIl\sin{\theta}\\ \end{aligned}\end{equation} $$ where $B$ is the magnetic flux density, $I$ is current, $l$ is the length of the wire, and $\theta$ is the angle between the wire and the field.
It is implied that longer conductors carrying larger currents will experience greater magnetic forces, given that flux density of the external magnet remains constant.
We use Fleming’s Left Hand (Motor) Rule to determine the direction in which the wire will be pushed. It is referred to as the Motor rule because it predicts the behaviour of a motor - the current and field are the inputs and the output is the spinning motion of the conductor.
Image Credits: How Electrical

The angle also matters as we’ll see in specific scenarios. We will next look at the flux patterns and magnetic forces associated with long straight wires, flat circular coils and long solenoids.
Force acting on a charge moving in a magnetic field
Given that a particle, charge $Q$ is moving at a speed $v$ at an angle $\theta$ relative to the field, the force $F$ exerted by the magnetic field on the particle is: $$ \begin{equation}\begin{aligned} F=BQv\sin{\theta}\\ \end{aligned}\end{equation} $$
