Given that the magnetic flux density $B$ is a measure of the amount of magnetic field that passes through unit area of a surface, the magnetic flux $\phi$ through an area $A$ is: $$ \begin{equation}\begin{aligned} \phi=BA\\ \end{aligned}\end{equation} $$
The angle that the field makes with the surface matters. If an angle of $\theta$ is formed between the normal to the surface and the field then the flux is given by $$ \begin{equation}\begin{aligned} \phi=BA\cos{\theta}\\ \end{aligned}\end{equation} $$
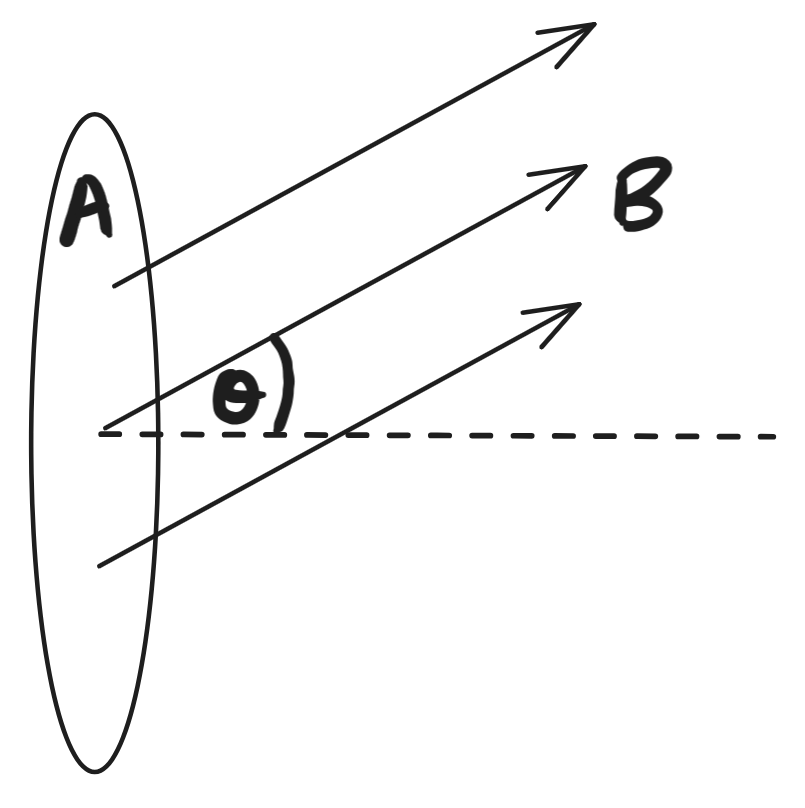
Magnetic flux’s SI unit is the weber (Wb), which the magnetic flux present when a magnetic flux density of 1 Tesla ($1 T$) passes through an area of $1 m^2$ at right angles: $$ \begin{equation}\begin{aligned} \phi&=BA\cos{\theta}\\ &\rightarrow 1T\times 1 m^2 \times \cos{90\degree}\\ &= 1Wb\\ \end{aligned}\end{equation} $$
Induced current and Fleming’s Right Hand Rule
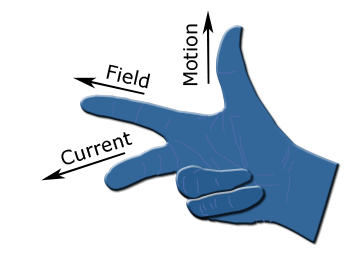
From using Fleming’s left hand rule, we understand that when a conductor is in a magnetic field, it will experience a force if it is carrying a current (force is the output when magnetic field and current are the inputs). If we have a magnetic field and the wire is made to move across the field, a current is created according to Fleming’s right hand rule.
When force and magnetic field are the inputs, an induced current is the output.
Image Credits: Wikipedia
Magnetic flux linkage
Where a solenoid is concerned, the flux is linked from each of the coils. For a solenoid with $N$ turns, the magnetic flux linkage is given as $$ \begin{equation}\begin{aligned} \text{linkage}= N\phi\\ \end{aligned}\end{equation} $$
Lenz’s Law of Electromagnetic Induction
This law states that the induced e.m.f. in a circuit flows in a direction such that it opposes the change that induced it.
Image Credits: Science Facts

Faraday’s Law of Electromagnetic Induction
The strength of the induced e.m.f. is directly proportional to the rate of change of magnetic flux linkage: $$ \begin{equation}\begin{aligned} E&\propto \frac{d}{dt}(N\phi)\\ E&=-N\frac{d\phi}{dt}\\ \end{aligned}\end{equation} $$
