A capacitor will behave differently depending on if there is a power source in the same loop. If a power source is present, the capacitor will charge. Otherwise it will discharge and behave like a power source itself.
Charging a capacitor
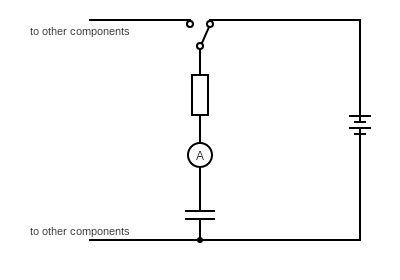
We usually charge a capacitor through a resistor:
Given that the voltages across the power supply, capacitor (capacitance $C$) and resistor (resistance $R$) are $V_S$, $V_C$ and $V_R$ respectively, we can write a relationship relating these voltages during capacitor charging: $$ \begin{equation}\begin{aligned} V_C=V_S(1-e^{-\frac{t}{CR}})\\ \end{aligned}\end{equation} $$
Because voltage and charge are proportional, charge, $Q$ stored in the capacitor behaves in a similar way: $$ \begin{equation}\begin{aligned} Q=Q_0(1-e^{-\frac{t}{CR}})\\ \end{aligned}\end{equation} $$
The current, $I$ in the loop, approaches zero as the capacitor’s voltage eventually matches that of the power supply: $$ \begin{equation}\begin{aligned} I=I_0e^{-\frac{t}{CR}}\\ \end{aligned}\end{equation} $$
As for the voltage across the resistor, the value decreases exponentially: $$ \begin{equation}\begin{aligned} V_R=V_0e^{\frac{-t}{CR}}\\ \end{aligned}\end{equation} $$
Discharging a capacitor
When the power source is removed from the loop by changing the position of the switch, the capacitor no longer charges. It discharges instead: $$ \begin{equation}\begin{aligned} Q=Q_0e^{\frac{-t}{CR}}\\ \end{aligned}\end{equation} $$
Time constant
The time constant is the value CR (the product of the capacitance of the capacitor and the resistance of the resistor in the same loop) seen in the exponent of $e$ in the various equations above. It represents the time taken for the charge on a capacitor to fall to $1/e$ of its initial value, $Q_0$. $$ \begin{equation}\begin{aligned} Q&=Q_0e^{\frac{-t}{CR}}\\ \frac{Q}{Q_0}&=e^{\frac{-t}{CR}}\\ \ln{\frac{Q}{Q_0}}&=\ln{e^{\frac{-t}{CR}}}\\ \ln{\frac{Q}{Q_0}}&=\frac{-t}{CR}\\ -\ln{\frac{Q}{Q_0}}&=\frac{t}{CR}\\ \ln{\frac{Q_0}{Q}}&=\frac{t}{CR}\\ CR&=\frac{t}{\ln{\frac{Q_0}{Q}}}\\ \end{aligned}\end{equation} $$
When the ratio $\frac{Q_0}{Q}=e$, $ln{\frac{Q_0}{Q}}=1$. Therefore when $Q=\frac{1}{e}Q_0$, $t=RC$.
The units of CR
Since it is the time for charge to drop to a certain value, CR must be a time value (and hence measured in seconds): $$ \begin{equation}\begin{aligned} CR&=\frac{Q}{V}\times \frac{V}{I}\\ &= \frac{Q}{I}=t\rightarrow s\\ \end{aligned}\end{equation} $$