If we know how resistance behaves in series and parallel: $$ \begin{equation}\begin{aligned} R_T&=R_1+R_2+R_3\\ \frac{1}{R_T}&=\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}\\ \end{aligned}\end{equation} $$ Then the opposite counts for capacitors in series and parallel. For series: $$ \begin{equation}\begin{aligned} \frac{1}{C_T}&=\frac{1}{C_1}+\frac{1}{C_2}+\frac{1}{C_3}\\ \end{aligned}\end{equation} $$
In parallel: $$ \begin{equation}\begin{aligned} C_T&=C_1+C_2+C_3\\ \end{aligned}\end{equation} $$
Deriving the effective capacitance for multiple capacitors placed in series
In series, the same amount of charge is built up across each capacitor, as well as the single capacitor that can be used to replace them: $$ \begin{equation}\begin{aligned} Q_T=Q_1=Q_2=Q_3\\ \end{aligned}\end{equation} $$
The voltage is also additive in series, as we know from Kircchoff’s Voltage Law: $$ \begin{equation}\begin{aligned} V_T=V_1+V_2+V_3\\ \end{aligned}\end{equation} $$
Each voltage can be divided by their respective charge because each charge is the same (it is fine to divide throughout by the same value): $$ \begin{equation}\begin{aligned} \frac{V_T}{Q_T}=\frac{V_1}{Q_1}+\frac{V_2}{Q_2}+\frac{V_3}{Q_3}\\ \end{aligned}\end{equation} $$ We know that $C=\frac{Q}{V}$ therefore $\frac{1}{C}=\frac{V}{Q}$ for each corresponding Q-V pair: $$ \begin{equation}\begin{aligned} \frac{1}{C_T}&=\frac{1}{C_1}+\frac{1}{C_2}+\frac{1}{C_3}\\ \end{aligned}\end{equation} $$
Deriving the effective capacitance for multiple capacitors placed in parallel
For capacitors in parallel, we know that charge splits up because current splits up in parallel (Kirchhoff’s Current Law): $$ \begin{equation}\begin{aligned} Q_T=Q_1+Q_2+Q_3\\ \end{aligned}\end{equation} $$
The voltage is the same in parallel: $$ \begin{equation}\begin{aligned} V_T=V_1=V_2=V_3\\ \end{aligned}\end{equation} $$
Combining these by dividing the charges by their respective voltages we get (dividing throughout by the same value): $$ \begin{equation}\begin{aligned} \frac{Q_T}{V_T}&=\frac{Q_1}{V_1}+\frac{Q_2}{V_2}+\frac{Q_3}{V_3}\\ \therefore C_T&=C_1+C_2+C_3\\ \end{aligned}\end{equation} $$
Challenge
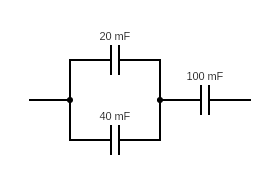
Find the capacitance of the single capacitor that can be used to replace the following system of capacitors:
