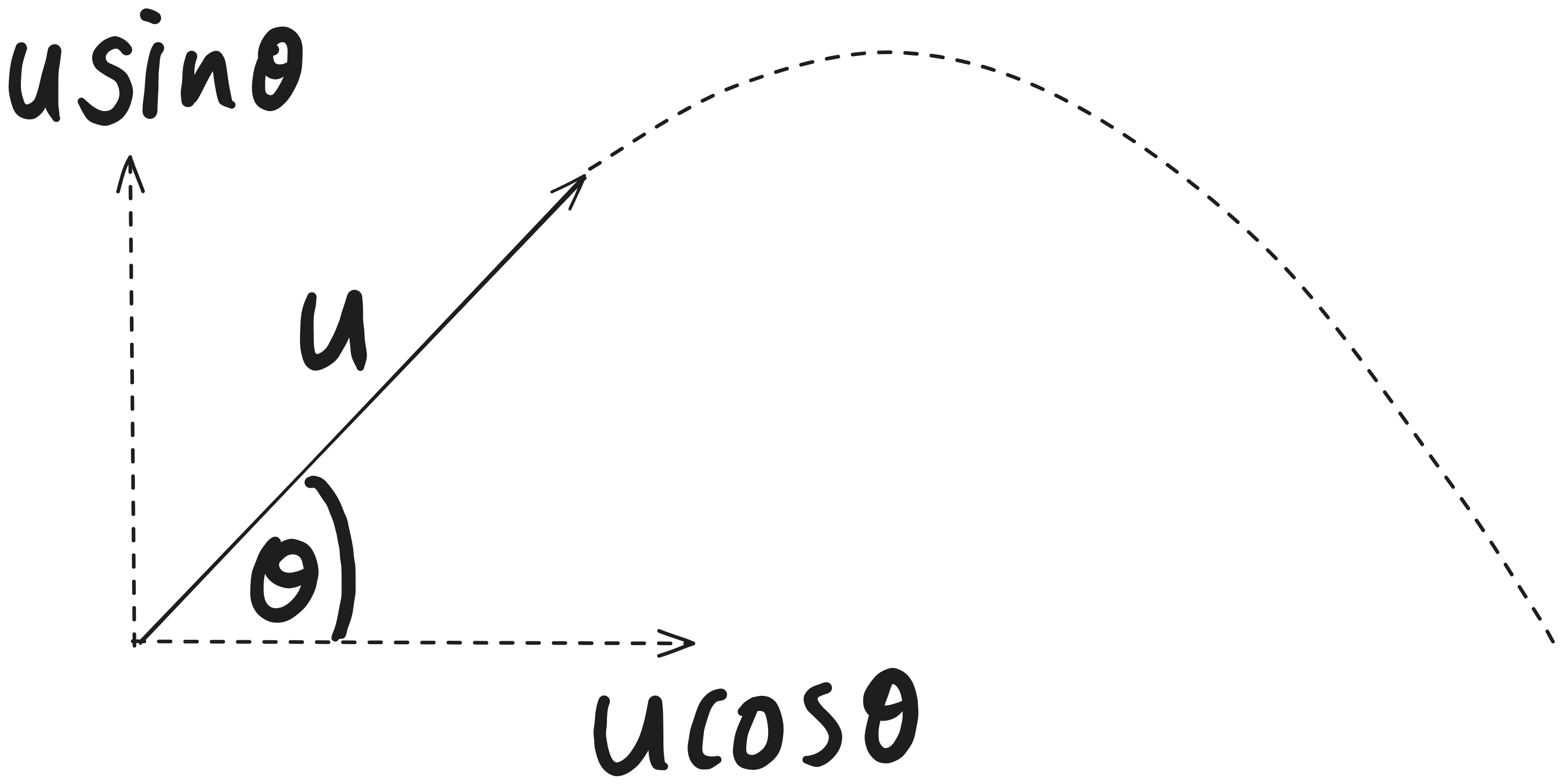
Projectile Motion

Projectile motion is essentially the motion of an object under the effect of gravity. Consider a projectile thrown at an angle of $\theta$ with an initial velocity of $u$:

View

Values that don’t change

We can resolve the initial velocity of the projectile into two perpendicular components: $$ \begin{equation}\begin{aligned} u_x&=u\cos{\theta}\\ u_y&=u\sin{\theta}\\ \end{aligned}\end{equation} $$ There are no horizontal forces acting and the only vertical force is gravity. Thus there is no horizontal acceleration and a vertical acceleration of $-g$: $$ \begin{equation}\begin{aligned} a_x&=0\\ a_y&=-g\\ \end{aligned}\end{equation} $$

Recap: the constant-acceleration equations of motion

Recall the following equations:

• $v=u+at$
• $s=(\frac{u+v}{2})t$
• $s=ut+\frac12at^2$
• $s=vt-\frac12at^2$
• $v^2=u^2+2as$

where

• $s$ is displacement,
• $u$ is initial velocity,
• $v$ is final velocity,
• $a$ is acceleration and
• $t$ is time

Time is the only scalar. The others are vectors so we apply a sign convention to them (usually vectors going up and right are positive and those going down and left are negative).

Applying the equations to projectiles

We can choose any of the equations of motion and apply them to a single direction. Because perpendicular vectors are independent, the horizontal motion is not affected by the vertical.

For example, let’s use $v=u+at$. Applying the equation to the horizontal(x) direction: $$v_x=u_x+a_xt$$ Substituting the values that don’t change: $$ \begin{equation}\begin{aligned} v_x&=u\cos{\theta}+(0)t\\ v_x&=u\cos{\theta}\\ v_x&=u_x\\ \end{aligned}\end{equation} $$ The final horizontal velocity($v_x$) is the same as the initial horizontal velocity($u_x$) because there is no horizontal acceleration($a_x=0$). If the projectile does not speed up or slow down in the x direction then why would the horizontal velocity change?

Applying the same equation to the vertical(y) direction: $$v_y=u_y+a_yt$$ Substituting the values that don’t change: $$ \begin{equation}\begin{aligned} v_y&=u\sin{\theta}+(-g)t\\ v_y&=u\sin{\theta}-gt\\ \end{aligned}\end{equation} $$

As the time passes, gravity causes the vertical component of the velocity to change so it makes sense for time($t$) to be part of the equation.

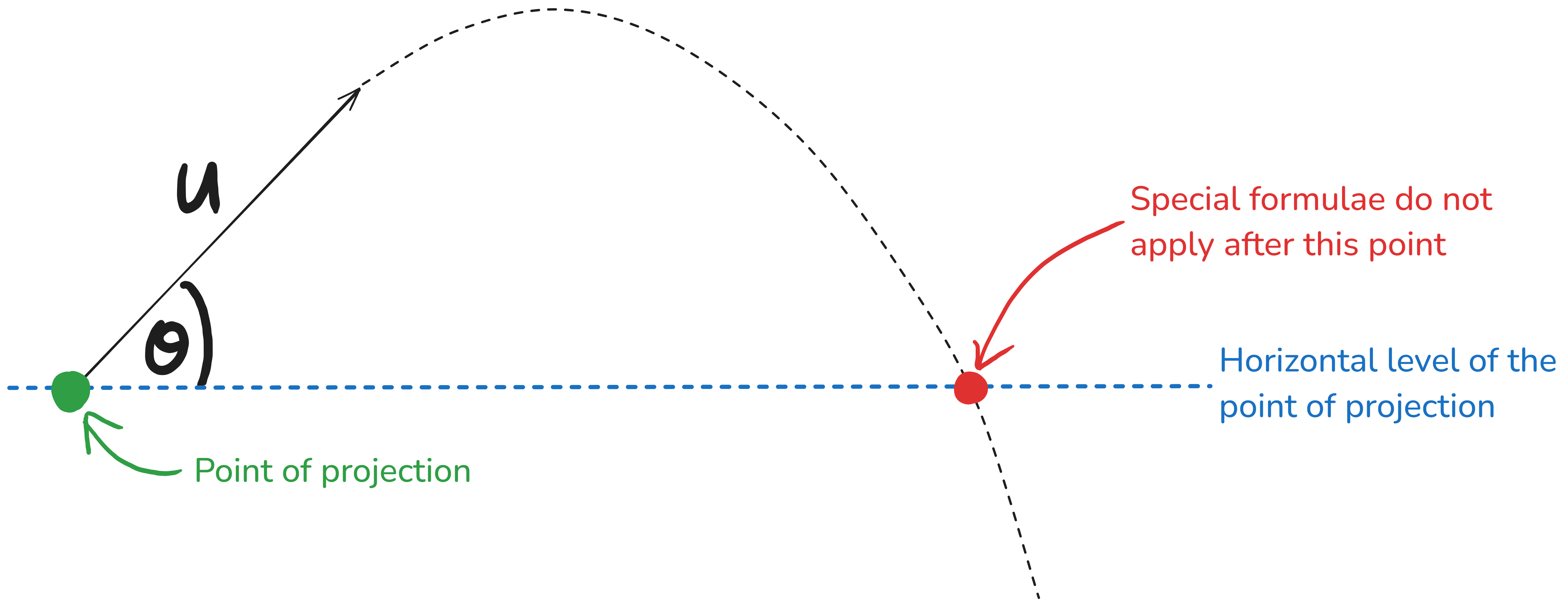
Special formulae

These are applied to projectiles from when they are launched to when they fall to the same horizontal level at which they were projected:

View

Time of flight

This is the time that the projectile stays up in the air before falling to the same horizontal level from which it was projected. $$ \begin{equation}\begin{aligned} \text{time of flight}=\frac{2u\sin{\theta}}{g}\\ \end{aligned}\end{equation} $$

Maximum height

This is the maximum displacement of the projectile above the horizontal level from which it was projected. $$ \begin{equation}\begin{aligned} \text{maximum height}=\frac{u^2\sin^2{\theta}}{2g}\\ \end{aligned}\end{equation} $$

Horizontal range

This is the horizontal displacement between the point of projection and the point at which the projectile falls to the same horizontal level from which it was projected. $$ \begin{equation}\begin{aligned} \text{horizontal range}=\frac{u^2\sin2{\theta}}{g}\\ \end{aligned}\end{equation} $$

1) What is the horizontal range of a projectile launched at $30 m/s$ at an angle of $45\degree$?

1. $0.00 m$
2. $22.9 m$
3. $91.7 m$
4. $4.32 m$

The formula for horizontal range is $\frac{u^2\sin{2\theta}}{g}$

2) If the time of flight of a projectile is 3 seconds, can the formula for maximum height be used at time 5 seconds?

1. Yes
2. No

The special formulae including maximum height can only be applied up until the time of flight (3 seconds)

3) If a projectile is projected horizontally, the maximum height formula will produce a value of 0.00 m

1. True
2. False

$\frac{u^2\sin^2{\theta}}{2g}$ evaluates to $0.00 m$ since $\theta=0\degree$ (the projectile being launched horizontally)