It is important to remember that the centripetal force is always the net force directed towards the center of the circle: $$F_{net}=\frac{mv^2}{r}$$
Horizontal circles
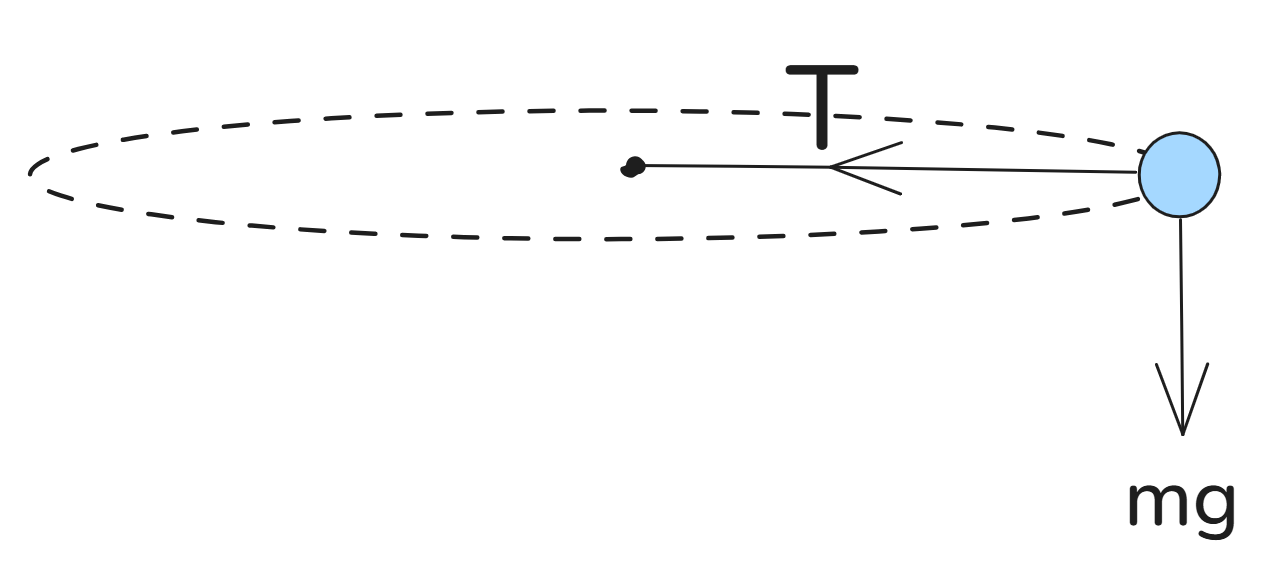
When an object revolves in a circular path around a point because of a force directed towards that point (the center of that circular path) and the circle is horizontal, the tension in the string keeps the object from flying off in any direction.
The centripetal force is thus given as: $$\frac{mv^2}{r}=T$$
The weight of the object has no effect on the tension as they are perpendicular (recall that perpendicular vectors are independent).
Vertical circles
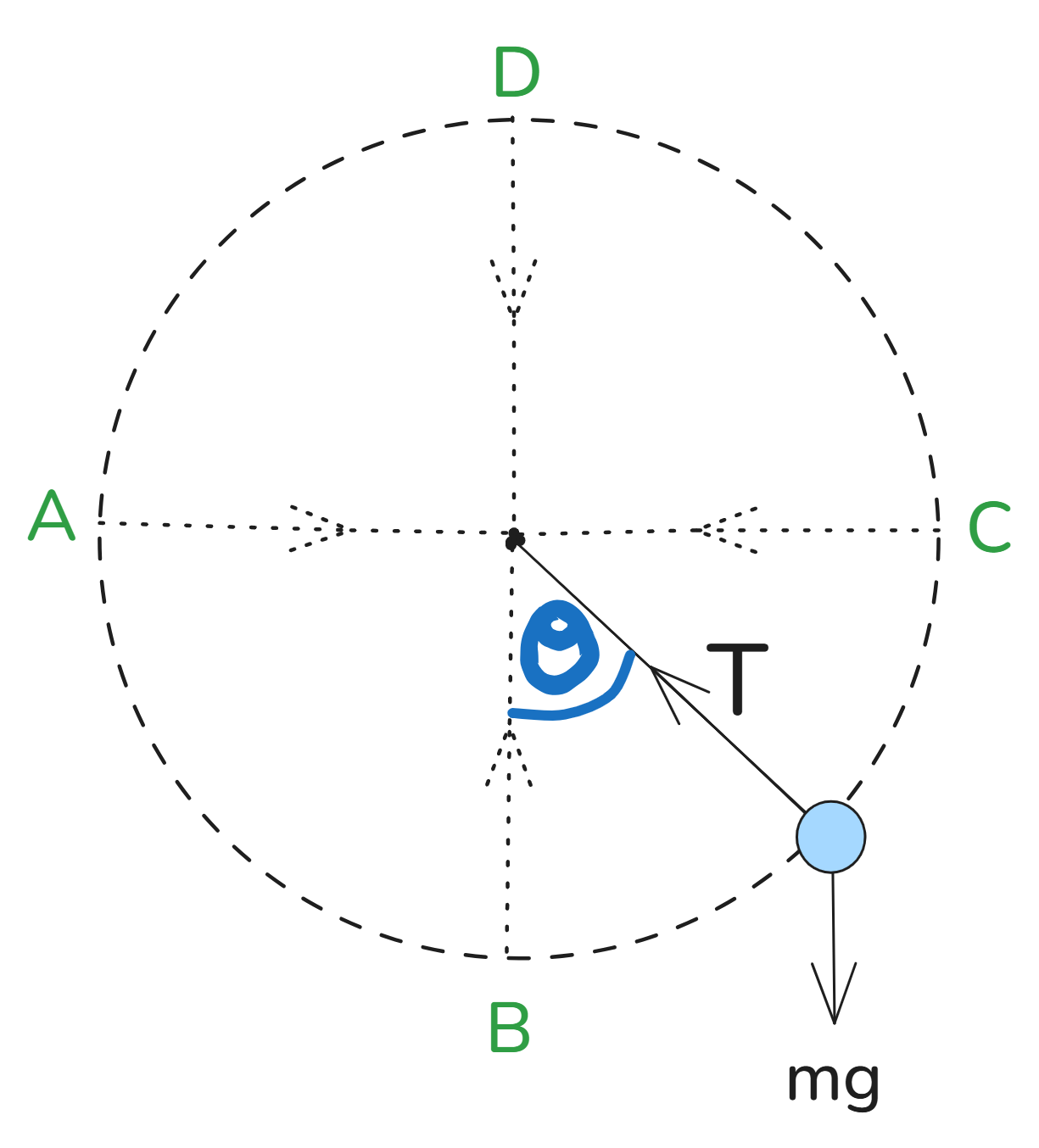
When the circle is vertical, we have to consider the effect of gravity on the tension in the string. In general, the centripetal force, written in terms of the tension, $T$, weight of the object, $mg$ and the angle, $\theta$ of the string relative to the vertical is: $$\frac{mv^2}{r}=T-mg\cos{\theta}$$
At C, $\theta=90\degree$: $$ \begin{equation}\begin{aligned} \frac{mv^2}{r}&=T-mg\cos{90\degree}\\ \frac{mv^2}{r}&=T\\ \end{aligned}\end{equation} $$
At D, $\theta=180\degree$: $$ \begin{equation}\begin{aligned} \frac{mv^2}{r}&=T-mg\cos{180\degree}\\ \frac{mv^2}{r}&=T+mg\\ \therefore T&=\frac{mv^2}{r}-mg\\ \end{aligned}\end{equation} $$
Here (at the highest point of the circular path) is where the tension is the least as gravity helps to keep the object moving in the circle.
At A, $\theta=270\degree$: $$ \begin{equation}\begin{aligned} \frac{mv^2}{r}&=T-mg\cos{270\degree}\\ \frac{mv^2}{r}&=T\\ \end{aligned}\end{equation} $$
At B, $\theta=0\degree$: $$ \begin{equation}\begin{aligned} \frac{mv^2}{r}&=T-mg\cos{0\degree}\\ \frac{mv^2}{r}&=T-mg\\ \therefore T&=\frac{mv^2}{r}+mg\\ \end{aligned}\end{equation} $$
Here (at the lowest point of the circular path) is where the tension is maximum as it needs to overcome gravity and also keep the object moving in the circle.
Conical pendulum
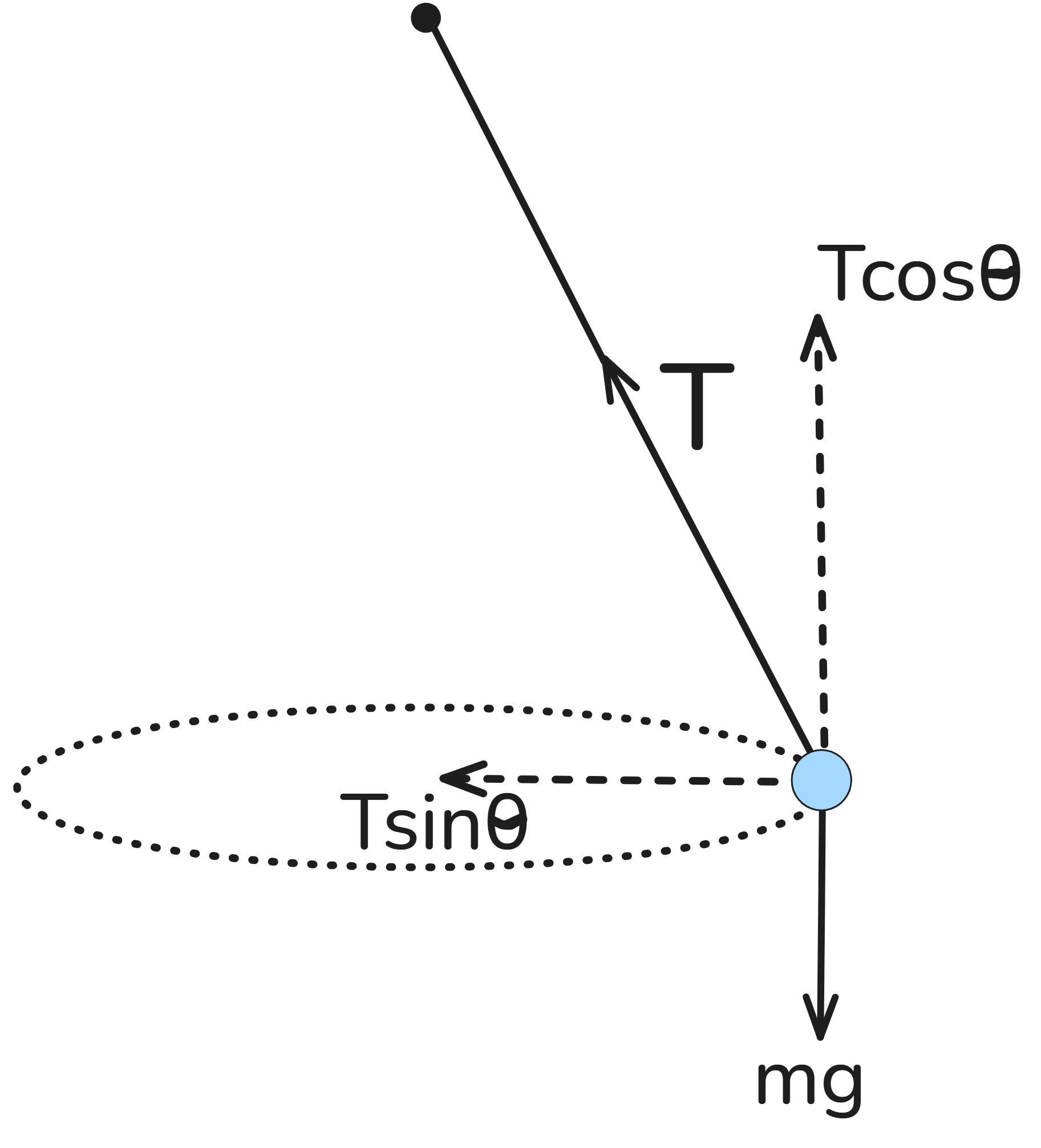
This is where the path traced out by a simple pendulum is not an arc but rather a circle:
The tension, $T$, acting at an angle, $\theta$ relative to the vertical, serves to both cancel out weight with its vertical component: $$T\cos{\theta}=mg$$ and have its horizontal component keep the bob moving in the circular path: $$\frac{mv^2}{r}=T\sin{\theta}$$
Dividing the latter equation by the former, we get: $$ \begin{equation}\begin{aligned} \frac{T\sin{\theta}}{T\cos{\theta}} &= \frac{mv^2}{r}\div mg\\ \frac{\sin{\theta}}{\cos{\theta}} &= \frac{mv^2}{r}\times\frac{1}{mg}\\ \tan{\theta} &= \frac{v^2}{rg}\\ \end{aligned}\end{equation} $$
Turning an aeroplane
The lift of an aeroplane is relative to the plane itself. The equations are similar to those for the conical pendulum except for the force serving to keep the plane in the circle of revolution being the lift from the plane.
$$L\cos{\theta}=mg$$ $$\frac{mv^2}{r}=L\sin{\theta}$$
$$ \begin{equation}\begin{aligned} \frac{L\sin{\theta}}{L\cos{\theta}} &= \frac{mv^2}{r}\div mg\\ \frac{\sin{\theta}}{\cos{\theta}} &= \frac{mv^2}{r}\times\frac{1}{mg}\\ \tan{\theta} &= \frac{v^2}{rg}\\ \end{aligned}\end{equation} $$Banked tracks
This is a track that slopes inwards towards the center of curvature. The equations are also similar to conical pendulum but the force is the reaction force from the track.
$$R\cos{\theta}=mg$$ $$\frac{mv^2}{r}=R\sin{\theta}$$
$$ \begin{equation}\begin{aligned} \frac{R\sin{\theta}}{R\cos{\theta}} &= \frac{mv^2}{r}\div mg\\ \frac{\sin{\theta}}{\cos{\theta}} &= \frac{mv^2}{r}\times\frac{1}{mg}\\ \tan{\theta} &= \frac{v^2}{rg}\\ \end{aligned}\end{equation} $$