We can find a value for absolute zero by doing:
- Vary the temperature of a gas under conditions of fixed pressure and take the respective volumes for each temperature
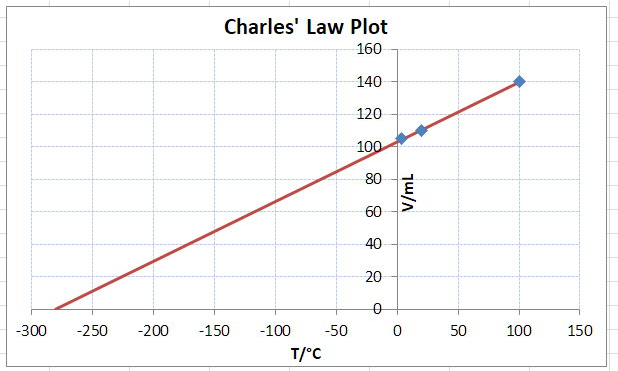
- Plot a graph of volume versus temperature and construct a best fit line
- Using the best fit line, extrapolate backwards to get the $x$ intercept (the value in degrees Celsius where the volume is zero)
Recall Charles’ Law: $$ \begin{equation}\begin{aligned} V\propto T\\ \end{aligned}\end{equation} $$ Introducing a constant of proportionality: $$ \begin{equation}\begin{aligned} V=kT\\ \end{aligned}\end{equation} $$ Comparing this to the straight line formula: $$ \begin{equation}\begin{aligned} \color{green}V&=\color{purple}k\color{red}T\color{gray}+0\\ \color{green}y&=\color{purple}m\color{red}x\color{gray}+c\\ \end{aligned}\end{equation} $$
Thus by plotting a graph of volume versus temperature, we can find the value at which the line cuts the $x\ axis$ (the temperature axis). This value corresponds to the temperature at which the gas would theoretically have a volume of zero. This value is absolute zero.
The same can be done for the Pressure Law:
- Vary the temperature of a gas under conditions of fixed volume and take the respective pressures for each temperature
- Plot a graph of pressure versus temperature and construct a best fit line
- Using the best fit line, extrapolate backwards to get the $x$ intercept (the value in degrees Celsius where the pressure is zero)
- The equation of the best fit line will be $P=kT+0$ (comparable to $y=mx+c$)
