Physical quantities can be divided into:
- Fundamental quantities vs. derived quantities OR
- Scalar quantities vs. vector quantities
We have looked at the former pair of categories. Now we shall study the latter.
Scalar quantities
Scalar quantities (or simply scalars) are physical quantities which have magnitude but NO direction. Examples include mass, length, time, distance and speed. When representing a scalar on a diagram, we simply write the measurement next to the corresponding object:
Vector quantities
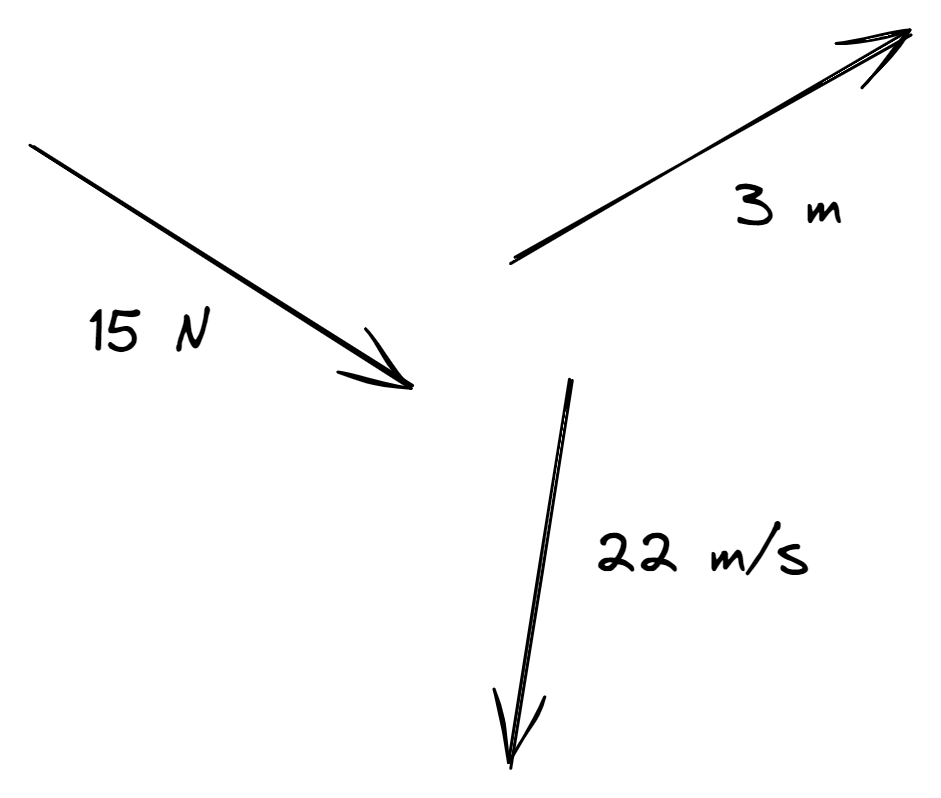
Vector quantities (or simply vectors) are physical quantities which have both magnitude AND direction. Examples include displacement, velocity, acceleration and force. We represent vectors with an arrow with the measurement next to it:
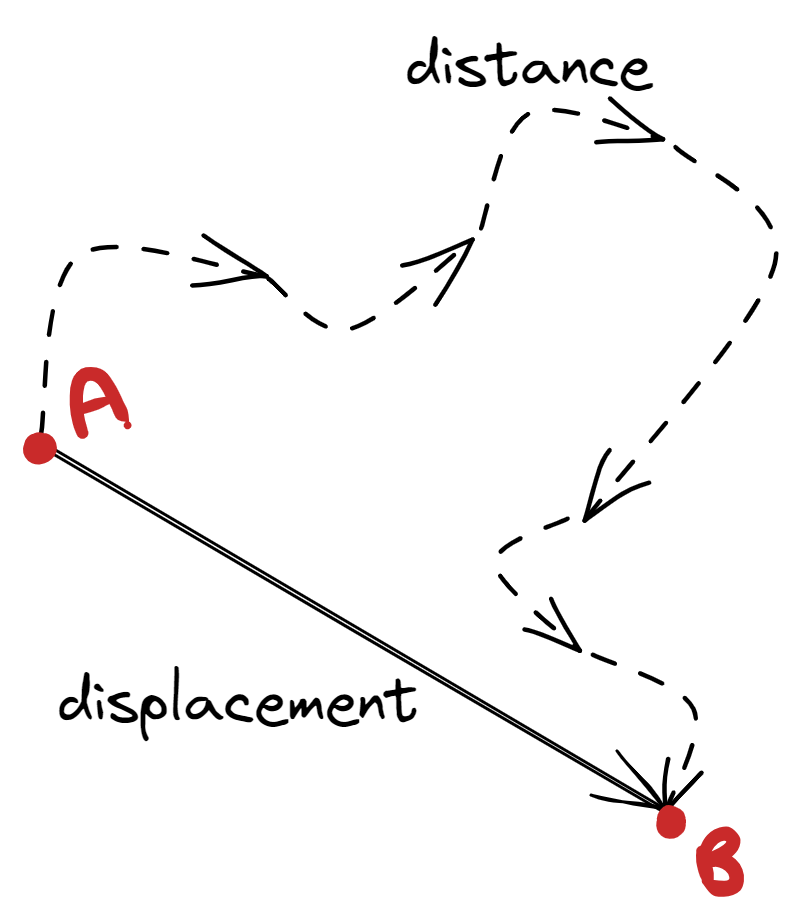
Example: Distance vs. Displacement
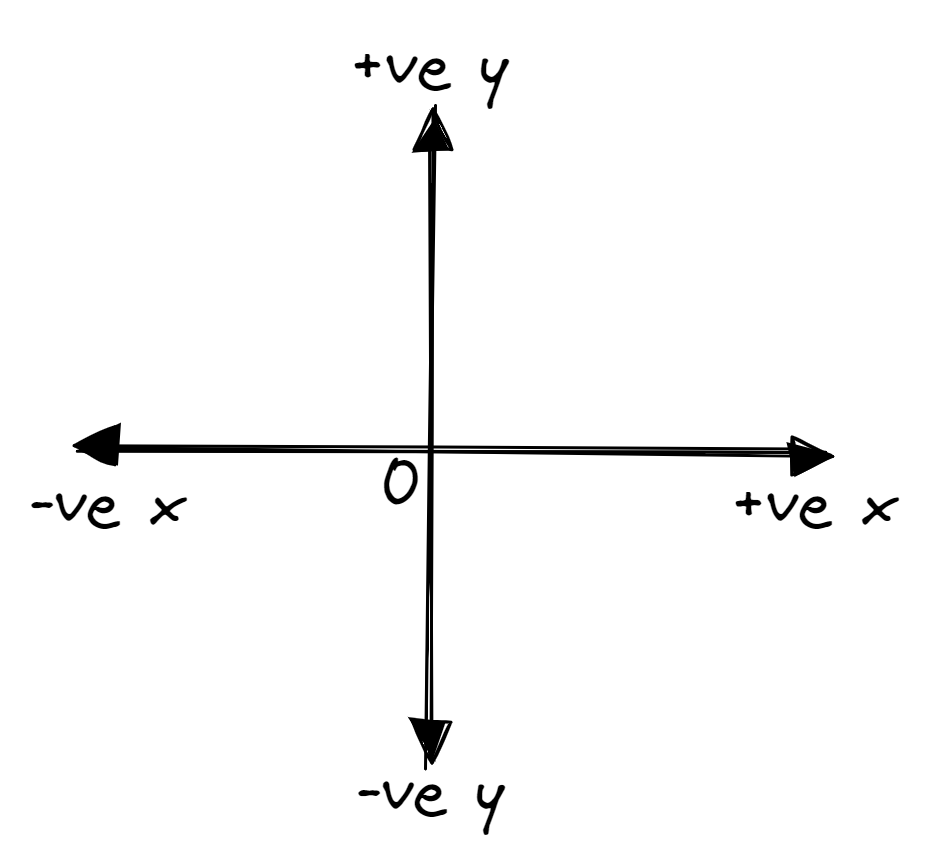
Sign conventions
A sign convention is a set of rules which specify the signs for certain directions. For example, a sign convention can dictate that on your book page all vectors going to the right are in the positive horizontal (x) direction and all vectors pointing downward are in the negative vertical (y) direction. In fact, the cartesian plane used in geometry does exactly that:
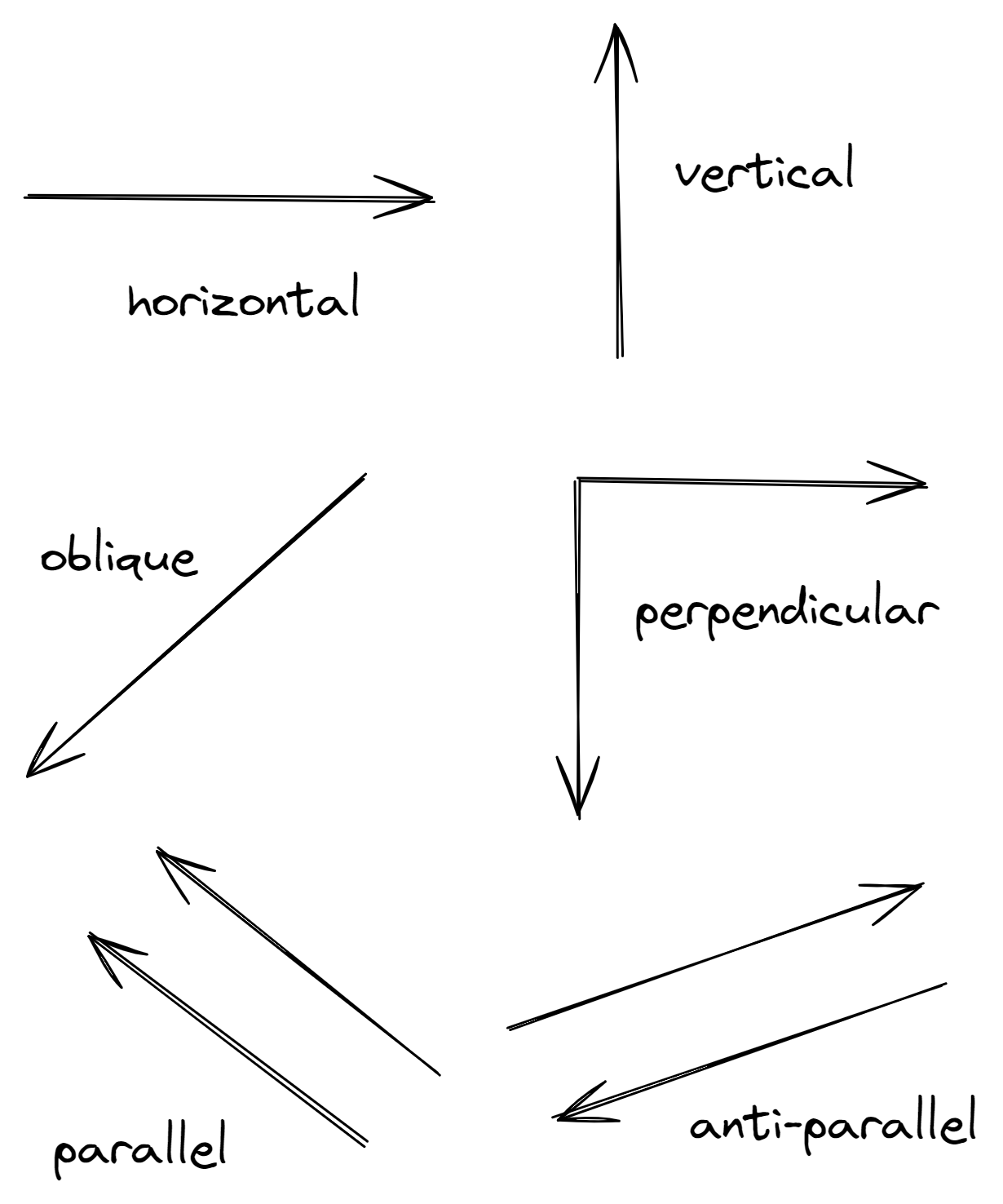
Types of vectors
We can describe vectors in terms of their direction:
- horizontal
- vertical
- oblique
We can also describe them relative to each other:
- perpendicular vectors
- parallel vectors
- anti-parallel vectors
Resolving vectors
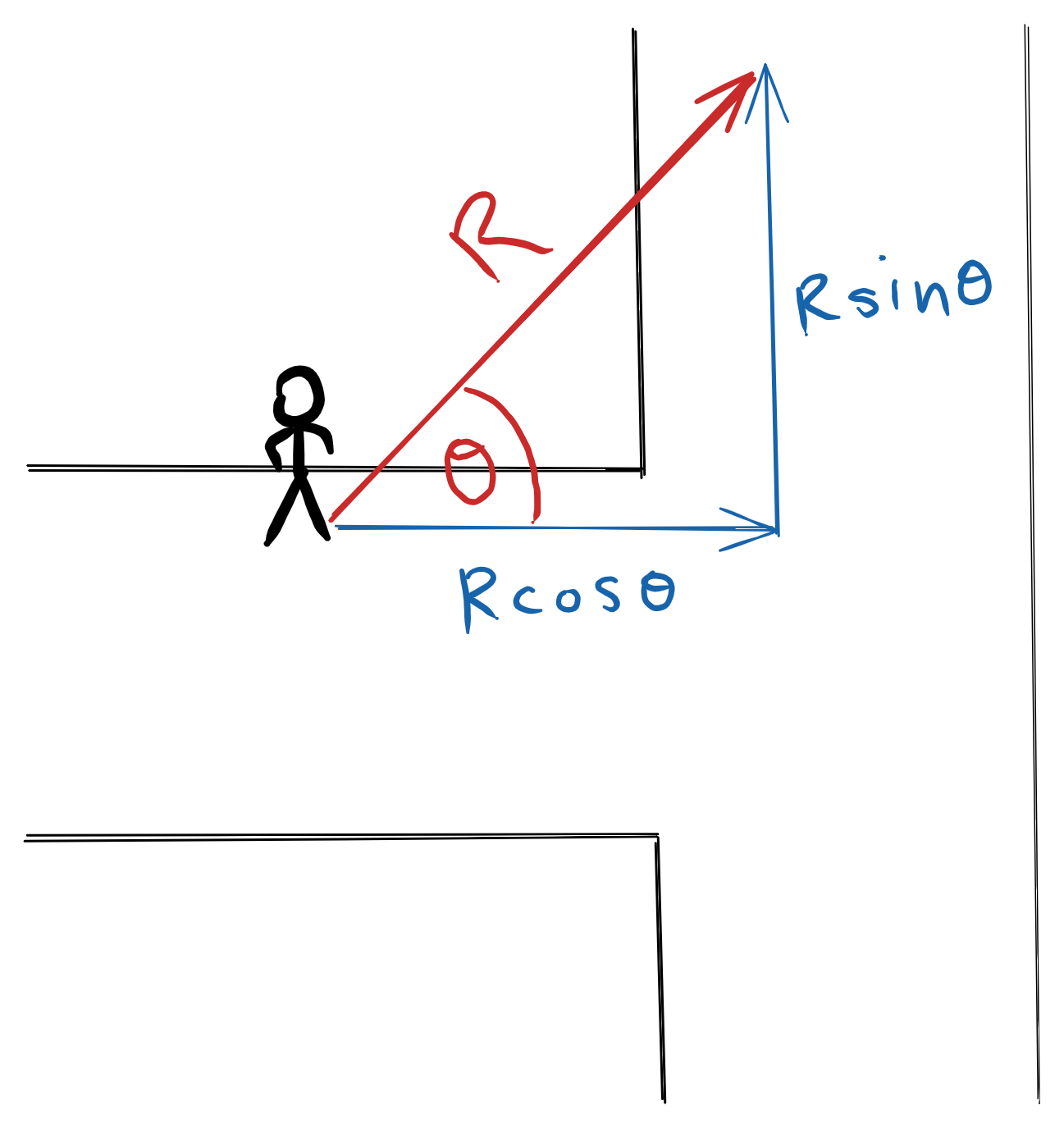
Imagine you normally take the red path (north-east) but one day it rains heavily and the shortcut area is flooded. How far would you have to walk east? How far would you have to walk north?
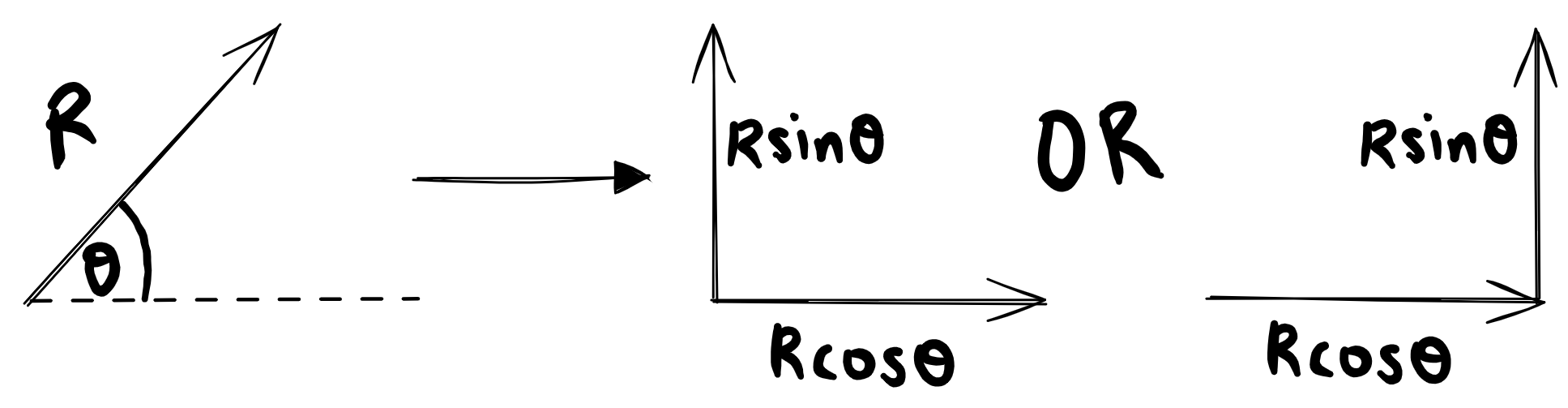
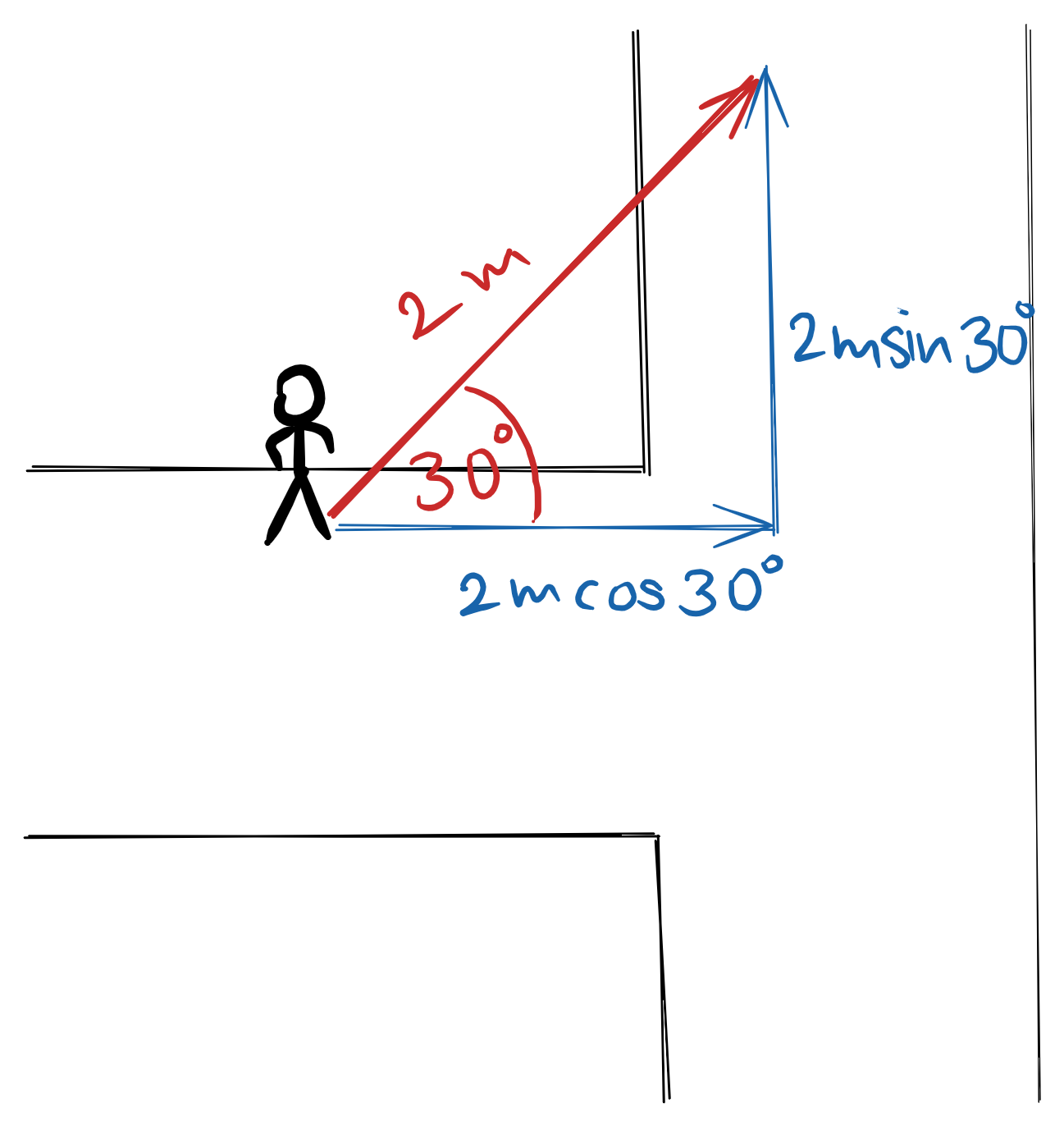
Any vector can be resolved into two (2) perpendicular components. The angle ($\theta$) that a vector forms with the horizontal or vertical must be known.
The adjacent component is always $Rcos\theta$. The other component is always $Rsin\theta$
Example
When we resolve vectors we are asking which two vectors can be used to replace the original vector. These two vectors MUST have the same overall effect as the original.
The components of a vector are themselves vectors
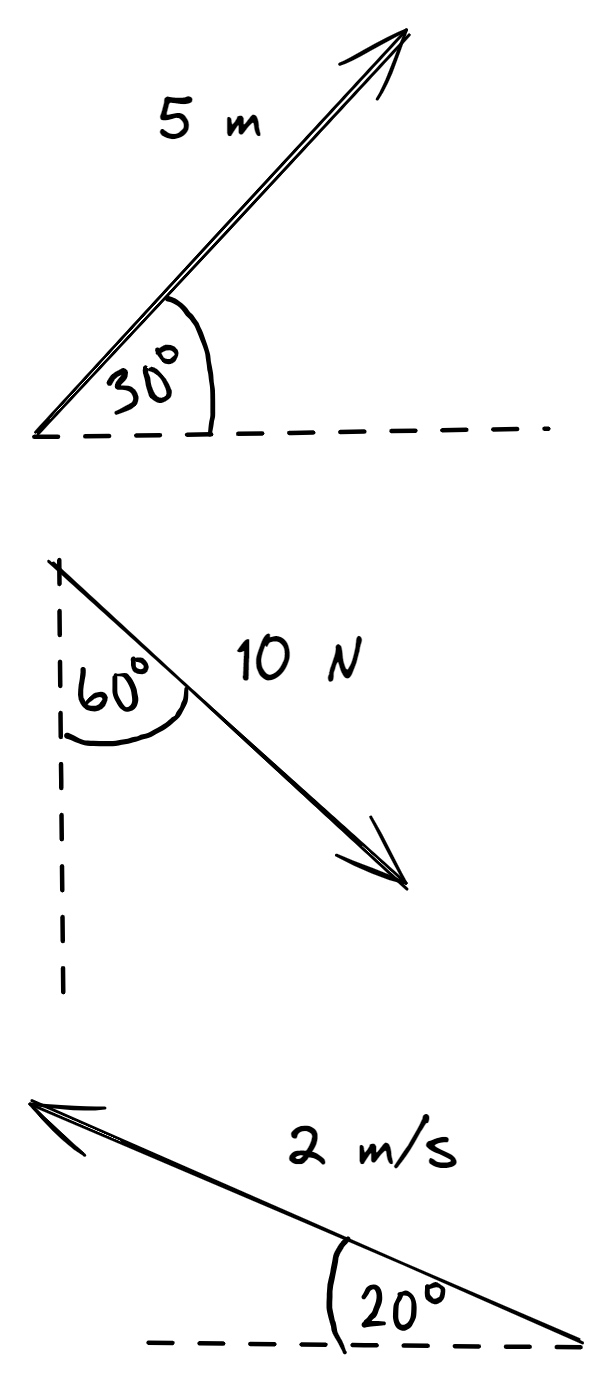
Mission details
Resolve the following vectors into two perpendicular components.