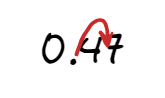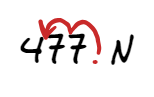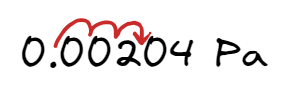Sometimes we want to represent very large or very small numbers efficiently. We use multiples and sub-multiples in order to avoid having to write too many digits.
Multiples
These are used to represent large numbers. Below are some commonly used multiples.
| Multiple prefix | Symbol | Value | Value expressed as a power of 10 |
|---|---|---|---|
| Kilo- | k | 1,000 | $10^3$ |
| Mega- | M | 1,000,000 | $10^6$ |
| Giga- | G | 1,000,000,000 | $10^9$ |
| Tera- | T | 1,000,000,000,000 | $10^{12}$ |
Notice that the prefixes are simply placeholders for positive (+ve) powers of 10.
Submultiples
These are used to represent small numbers. Below are some commonly used submultiples.
| Submultiple prefix | Symbol | Value | Value expressed as a power of 10 |
|---|---|---|---|
| Milli- | m | 0.001 | $10^{-3}=\frac{1}{10^3}=\frac{1}{1,000}$ |
| Micro- | $\mu$ | 0.000001 | $10^{-6}=\frac{1}{1,000,000}$ |
| Nano- | n | 0.000000001 | $10^{-9}=\frac{1}{1,000,000,000}$ |
| Pico- | p | 0.000000000001 | $10^{-12}=\frac{1}{1,000,000,000,000}$ |
Here the prefixes are used to represent negative (-ve) powers of 10.
How we use multiples and submultiples
We place the prefix of the multiple or submultiple after the magnitude to modify the unit. $$ \begin{equation}\begin{aligned} \text{magnitude}\times \text{unit}\rightarrow& \color{limegreen}\text{different\ magnitude}\color{black}\\ &\times \color{slateblue}\text{prefix}+\text{unit}\\ e.g.\ 3000\ \text{grams}\rightarrow& \color{limegreen}3\color{normal}\times \color{slateblue}\text{kilogram}\\ \end{aligned}\end{equation} $$ It should be noted that we do not stack prefixes so you won’t see anything like kilomegagram. Kilo- means 1,000 and mega- means 1,000,000 and 1,000 of 1,000,000 is 1,000,000,000 or giga- in short. Thus gigagram is more viable.
Standard form/Scientific notation
When converting from one unit to another, remember that the prefixes for multiples and sub-multiples are simply powers of 10 in disguise. For example, look at the kilogram: $$ \begin{equation}\begin{aligned} kilogram\rightarrow kilo-gram\rightarrow 10^{3}\ grams\rightarrow 1000\ grams\\ \end{aligned}\end{equation} $$ Because the metric system of measurement is based on powers of 10, it is important for us to understand standard form.
What is standard form?
This is when we write numbers in the form $$ a\times 10^b $$ Where $a$ is the coefficient and $b$ is the power/exponent of 10. $a$ must be a single non-zero digit (at least 1 but less than 10), ignoring any negative sign.
Shifting the decimal point to the left by 1 digit increases the power of 10 by 1 Shifting the decimal point to the right by 1 digit decreases the power of 10 by 1
Examples
- Write 20,000 in standard form$$ \begin{equation}\begin{aligned} 20,000\rightarrow20,000\times 10^0\rightarrow 2.0\times 10^4\\ \end{aligned}\end{equation} $$
- Write 0.47 in standard form$$ \begin{equation}\begin{aligned} 0.47\rightarrow 0.47\times 10^0\rightarrow 4.7\times 10^{-1}\\ \end{aligned}\end{equation} $$
- Write 477 N in standard form$$ \begin{equation}\begin{aligned} 477\ N\rightarrow 477\times 10^0\ N\rightarrow4.77\times 10^2\ N\\ \end{aligned}\end{equation} $$
Notice that the standard form is used for the magnitude of the measurement. The unit is unaffected.
- Write 0.00204 Pa in scientific notation
Mission details
Write the following measurements in standard form/scientific notation:
- $1300\ g$
- $0.004\ km$
- $5,031\ A$
- $0.0000678\ ms^{-2}$
1) Whenever we shift the decimal point to the left, we must decrease the power of 10
- True
- False
2) Every multiple is used to represent a power of 10
- True
- False