The moment of a force is the turning effect of that force. It is dependent on:
- The magnitude and direction of the force
- The position of the force’s line of action relative to the pivot
The moment of a force is given by $$ \begin{equation}\begin{aligned} moment=&\text{force}\times\text{perpendicular}\\ &\text{distance between line}\\ &\text{of action of force and pivot}\\ \end{aligned}\end{equation} $$
Example
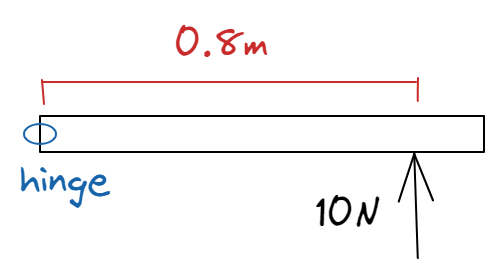
James pushes a door at the door knob which is located $0.8\ m$ away from the door’s hinge. If he pushes the door with a force of $10\ N$, find the moment of the force.
$$ \begin{equation}\begin{aligned} moment&=force\times perp.\ distance\\ &=10\ N\times 0.8\ m\\ &=8\ Nm\\ \end{aligned}\end{equation} $$Note that the moment of a force has an SI unit of Newton-metre ($Nm$).
Principle of moments
The principle of moments states that for a body in equilibrium, the sum of anti-clockwise moments is equal to the sum of clockwise moments: $$ \begin{equation}\begin{aligned} \sum ACW\ moments&=\sum CW\ moments\\ \end{aligned}\end{equation} $$