Theory
Momentum is a vector quantity which is expressed as the product of the mass and the velocity of an object. $$momentum(p)=mv$$
Impulse can be defined as a change in momentum of the object. It is essentially the time-effect of a force. Think about how a cricketer catches and slows down a ball by relaxing the arms rather than keeping them rigid. The effect of applying this retarding force over a time interval changes the momentum of the ball from its maximum value to zero. $$ \begin{equation}\begin{aligned} impulse&=force\times time\\ \Delta p &= Ft\\ \end{aligned}\end{equation} $$
This equation can also be expanded to give $$ \begin{equation}\begin{aligned} \Delta p=Ft&=\frac{m(v-u)}{t} t\\ &=m(v-u)\\ &=mv-mu\\ \end{aligned}\end{equation} $$
The impulse of an object under a constant force is calculated using these formulae. In the case of an object under a varying force, a force-time graph can be used – such graphs can also be used to represent constant forces. The area under a force-time graph is the impulse for the object.
The principle of conservation of momentum dictates that the total momentum before a collision is equal to the total momentum after that collision, given that there are no external forces acting. A collision may be elastic where kinetic energy is conserved or inelastic where kinetic energy is lost. Regardless of the type of collision, momentum is conserved.
Elasticity($k$) is the ratio of the magnitudes of the relative velocities of the objects after and before collision:
$$ \begin{equation}\begin{aligned} k=\left|\frac{v_2-v_1}{u_2-u_1}\right|\\ \end{aligned}\end{equation} $$Where $v$ is the final velocity and $u$ is the initial velocity, with the subscript indicating the object number.
Note: The modulus of a value $x$ (written as $\left|x\right|$) is simply the positive version of that value (just drop the minus sign if there is one).
Aim
To investigate the relationship among the velocities and kinetic energies of objects and the elasticity of their collisions
Materials/Apparatus
Diagram
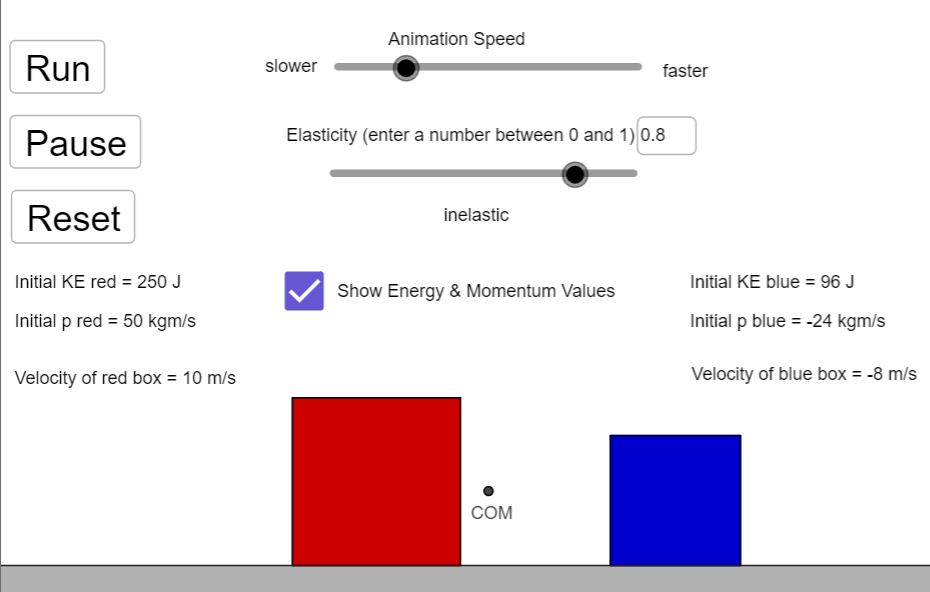
Method
- Run the simulation here
- Ensure the mass of the red box is set to 5 kg and that of the blue box is set to 3 kg
- Set the initial velocity of the red box to 10 m/s and that of the blue box to -10 m/s
- Set the elasticity of the collision to 1
- Record the initial velocities and kinetic energies
- Run the simulation and pause it after the collision
- Record final velocities and kinetic energies
- Reset the simulation and repeat steps 3 to 7 for other combinations of initial velocities and elasticity values as indicated in the table below
Results
| Initial velocity of red box($u_1$)/$ms^{-1}$ | Initial velocity of blue box($u_2$)/$ms^{-1}$ | Elasticity of collision | Total momentum before collision/$kgms^{-1}$ | Initial KE of red box/$J$ | Initial KE of blue box/$J$ | Total initial KE/$J$ | Final velocity of red box($v_1$)/$ms^{-1}$ | Final velocity of blue box($v_2$)/$ms^{-1}$ | Total momentum after collision/$kgms^{-1}$ | Final KE of red box/$J$ | Final KE of blue box/$J$ | Total final KE/$J$ | $u_2-u_1$ | $v_2-v_1$ | $k$ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 10 | -10 | 1.0 | |||||||||||||
| 10 | -10 | 0.5 | |||||||||||||
| 10 | -8 | 1.0 | |||||||||||||
| 10 | -8 | 0.5 | |||||||||||||
| 10 | -6 | 1.0 | |||||||||||||
| 10 | -6 | 0.5 |
Data Analysis
- In each case, did the value of the elasticity of the collision set in the experiment match that of k?
- What is the relationship between the initial total KE and the final total KE where the elasticity of collision is 1? Were they equal when the elasticity was 0.5?
- Does the elasticity of collision have a relationship with the relative velocities? What is this relationship?
- In each case, can we say that the total momentum before collision was equal to that after collision? Is the conservation of linear momentum independent of the elasticity of the collision?
