The following lab can be replicated in person by using a metre rule, masses with mass holders and a spring.
Theory
Hooke’s law states that the deformation of an object is directly proportional to the force applied, and is given by the formula $$F=kx$$ where the extension ($x$) is $$x=current\ length-original\ length$$
We can make $x$ the subject of the formula and write it in the form of a straight line equation: $$ \begin{equation}\begin{aligned} x&=\frac{F}{k}\\ \color{limegreen}x&=\color{royalblue}\frac1k\color{red}F\color{normal}+0\\ \color{limegreen}y&=\color{royalblue}m\color{red}x\color{normal}+c\\ \end{aligned}\end{equation} $$
Thus if we plot a graph of extension ($x$) versus force ($F$), we get a y-intercept of $0$ and a gradient which is the reciprocal of the spring constant($\frac{1}{k}$): $$m=\frac{1}{k}$$
Thus the spring constant $$k=\frac{1}{m}$$ where the units of the gradient $m$ will be $m/N$, meaning the units for $k$ will be $N/m$.
Aim
To find the spring constant of a spring using Hooke’s Law
Materials/Apparatus
Diagram
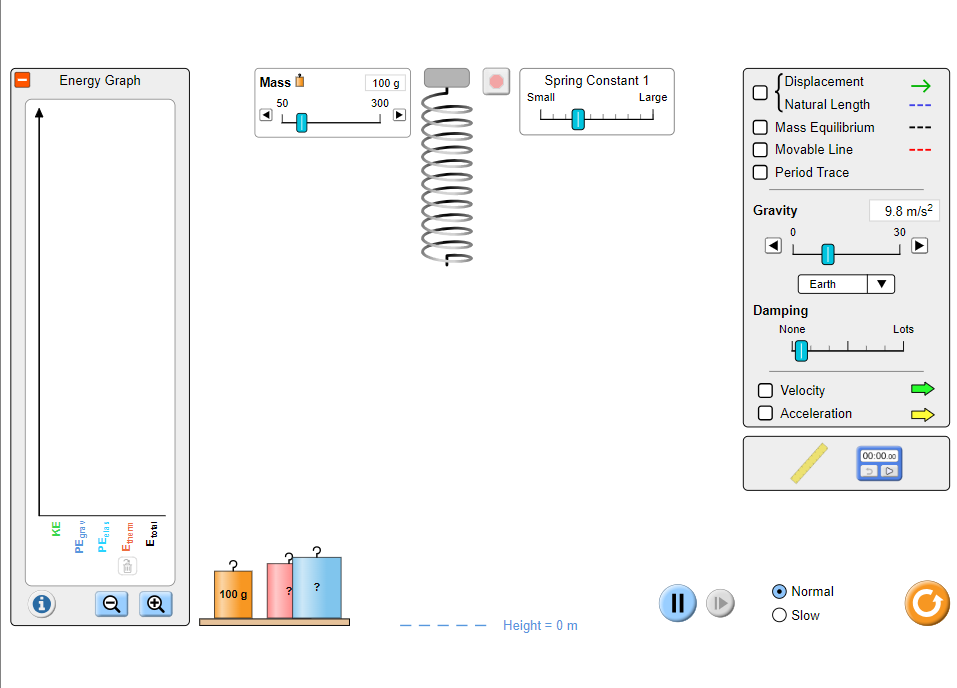
Method
- Run the simulation
- Choose the ‘Lab’ option
- Set the damping to ‘Lots’
- Use the ruler to measure and record the original length of the spring
- Hang the mass onto the spring and set the mass to 100 grams
- If the mass is oscillating let it come to rest before taking any measurements
- Measure and record the new length of the spring
- Repeat steps 4 to 6 for masses 120 grams to 200 grams at regular intervals of 20 grams
Results
| Mass/$kg$ | Weight/$N$ | Length of spring/$mm$ | Extension/$mm$ | Extension/$m$ |
|---|---|---|---|---|
| 0.00 | ||||
| 0.10 | ||||
| 0.12 | ||||
| 0.14 | ||||
| 0.16 | ||||
| 0.18 | ||||
| 0.20 |
Data Analysis
- Plot a graph of extension (on the y axis) versus force (on the x axis)
- Calculate the spring constant using the gradient of the graph
