Deformation can be defined as any change in shape caused by the application of a force. There are 2 types of deformation:
- Elastic/temporary deformation - in which the object returns to its original shape after the force is removed
- Plastic/permanent deformation - the object does not revert to its original shape. It may remain in the shape it was in when the force was present (as seen in modelling clay) or may revert only partially to the original shape (like an overstretched elastic band which has not been stretched enough to burst)
Hooke’s Law
Hooke’s Law states that the deformation of an object is directly proportional to the force applied. In other words, as we increase/decrease the force on the object, the deformation seen in the object will increase/decrease respectively. In the case of a spring, the deformation is the spring’s extension($x$), the change in the spring’s length ($x=current\ length-original\ length$):
$$F\propto x$$
$$F=kx$$
In the case of the object being a spring, this constant $k$ is called the spring constant. It’s unit can be derived from the formula: $$k=\frac{F}{x}\rightarrow \frac{N}{m}\ OR\ Nm^{-1}$$ The possible units are $N/m$, $N/cm$ or $N/mm$. This is a deviation from the usual convention to represent quantities in standard units. The force will almost always be measured in Newtons but the extension’s units vary based on the object being measured – it would be difficult imagining the extension of a small rubber band in metres or that of a large slinky in millimetres.
Force-extension graphs
The force-extension graph shows the relationship between the force applied to an object and the resulting extension observed in the object. The limit of proportionality is the point past which the graph no longer obeys Hooke’s Law. The elastic limit is the point after which plastic deformation is seen in the material.
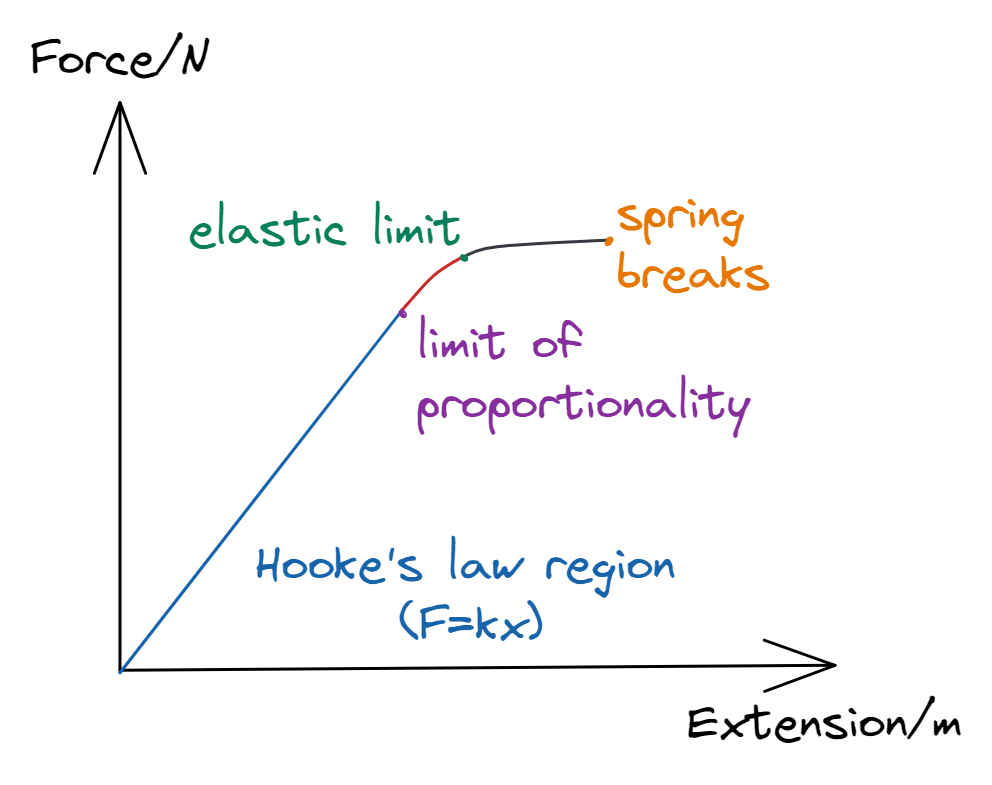
Notice that the manipulated variable is placed on the x axis and the responding variable is placed on the y axis.
Example
What is the magnitude of the force required to stretch a 20 cm-long spring, with a spring constant of 100 N/m, to a length of 21 cm?
$$x=(21-20)cm=1\ cm = 0.01\ m$$ $$k=100\ N/m$$ $$F=kx=100\ N/m \times 0.01\ m=1\ N$$
Mission details
What is the spring constant, in N/m, of a spring that needs a force of 3 N to be stretched from 35 cm to 40 cm?
