Energy is the ability to do work. It has the same SI unit as work - Joules(J). Some forms of energy are:
- gravitational potential
- kinetic
- elastic
- chemical
- electrical
- magnetic
- electromagnetic (light)
- thermal
- nuclear
- sound
Law of conservation of energy
Energy is neither created nor destroyed but it changes in form.
Examples of energy conversion
- In an electric motor, electrical energy from the battery is transformed into kinetic energy of the rudder
- In a hydroelectric dam, the gravitational potential energy of the water at the top of the dam is converted to kinetic energy as the water falls to the bottom and that is used to turn turbines which convert this kinetic energy to electrical energy
- In a battery, chemical energy is converted to electrical energy
- In an incandescent light bulb, electrical energy is converted to both light energy and thermal energy
- Speakers convert electrical signals into sound energy
- When a vehicle comes to a stop, its kinetic energy is converted to thermal energy
- When food is cooked in a microwave oven, electrical energy is converted to electromagnetic energy and this in turn is converted into thermal energy
- Solar panels convert electromagnetic energy from the sun into electrical energy
- Kinetic energy of wind is converted to electrical energy by wind turbines
Types of mechanical energy
Mechanical energy is divided into two (2) types:
- Potential energy
- Kinetic energy
Potential energy
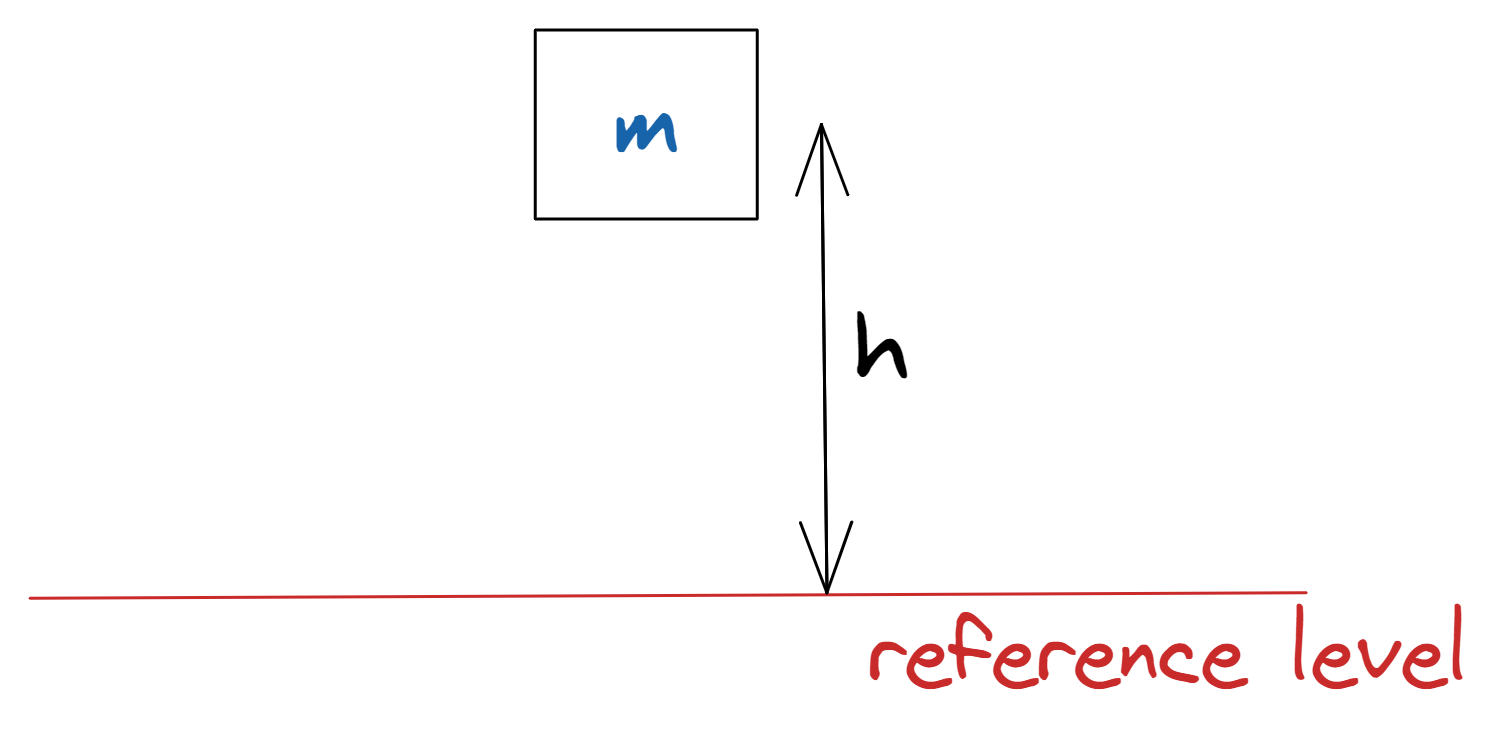
This is the energy a body possesses by virtue of its position within a field or system or its state. We will focus on gravitational potential energy (GPE) - the energy a body has by virtue of its position in the Earth’s gravitational field. GPE is given by the formula $$ \begin{equation}\begin{aligned} GPE=mgh\\ \end{aligned}\end{equation} $$ where $m$ is the object’s mass, $g$ is acceleration due to gravity and $h$ is the height of the object above the reference level, usually taken as the ground.
A change in GPE is given by the formula $$ \begin{equation}\begin{aligned} \Delta GPE&=GPE_f-GPE_i\\ &=mgh_f-mgh_i\\ &=mg(h_f-h_i)\\ &=mg\Delta h\\ \end{aligned}\end{equation} $$
Example
A ball falls from a height of $5\ m$ to that of $3\ m$ above the ground. If the mass of the ball is $4\ kg$, find the change in gravitational potential energy. $$ \begin{equation}\begin{aligned} \Delta GPE&=mg\Delta h\\ &=4\ kg\times9.81\ ms^{-2}\times(3\ m-5\ m)\\ &=-78.48\ kgm^2s^{-2}\ OR\ -78.48\ J\\ \end{aligned}\end{equation} $$ This means that the ball lost $78.48\ J$ of GPE.
Kinetic energy
This is the energy a body possesses by virtue of its motion. The kinetic energy (KE) is dependent on the mass ($m$) and velocity ($v$) of the object: $$ \begin{equation}\begin{aligned} KE=\frac{1}{2}mv^2\\ \end{aligned}\end{equation} $$ A change in KE is given by the formula $$ \begin{equation}\begin{aligned} \Delta KE&=KE_f-KE_i\\ &=\frac{1}{2}mv_f^2-\frac{1}{2}mv_i^2\\ &=\frac{1}{2}m(v_f^2-v_i^2)\\ \end{aligned}\end{equation} $$
Example
Find the kinetic energy of a ball of mass $2\ kg$ and velocity $4\ ms^{-1}$. $$ \begin{equation}\begin{aligned} KE&=\frac{1}{2}mv^2\\ &=\frac{1}{2}(2\ kg)(4\ ms^{-1})^2\\ &=\frac{1}{2}(2\ kg)(16\ m^2s^{-2})\\ &=16\ kgm^2s^{-2}\ OR\ 16\ J\\ \end{aligned}\end{equation} $$
Conservation of mechanical energy
If an object of mass $m$ is released from a height $h$, its potential energy is gradually converted to kinetic energy as it falls such that $$ \begin{equation}\begin{aligned} GPE\ at\ the\ top&=KE\ at\ the\ bottom\\ mg\Delta h&=\frac{1}{2}mv^2\\ g\Delta h&=\frac{1}{2}v^2\\ v^2&=2g\Delta h\\ v&=\sqrt{2g\Delta h}\\ \end{aligned}\end{equation} $$
Example 1
Find the final velocity of a box with mass $0.5\ kg$, just before it hits the ground, falling from a height of $3\ m$. $$ \begin{equation}\begin{aligned} v&=\sqrt{2g\Delta h}\\ &=\sqrt{2(9.81\ ms^{-2})(3\ m-0\ m)}\\ &=\sqrt{58.86\ m^2s^{-2}}\\ &=7.67\ ms^{-1}\\ \end{aligned}\end{equation} $$
Example 2
What would be the height of release if the box were to have a final velocity of $9\ ms^{-1}$ just before it hits the ground? $$ \begin{equation}\begin{aligned} v&=\sqrt{2g\Delta h}\\ \Delta h&=\frac{v^2}{2g}\\ h_2-h_1&=\frac{v^2}{2g}\\ h_2&=\frac{v^2}{2g}+h_1\\ h_2&=\frac{(9\ ms^{-1})^2}{2(9.81\ ms^{-2})}+0\ m\\ &=4.13\ m\\ \end{aligned}\end{equation} $$
The greater the height the object is released from, the greater the final velocity.