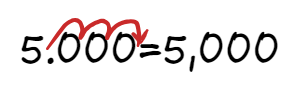Recall that when doing standard form, we can shift the decimal point to the left and increase the power of 10. We can also shift the decimal point to the right and decrease the power of 10. Doing these in the opposite order is also valid:
If we increase the power of 10 by 1 then we MUST shift the decimal point to the left by 1 digit If we decrease the power of 10 by 1 then we MUST shift the decimal point to the right by 1 digit
The following method of doing conversions exploits these two rules.
Converting from one unit to another
Let’s look at a few examples.
- Convert 5 Mg to kg
We write 5 Mg with the prefix as a power of $10$: $$\begin{gathered} 5\ Mg\rightarrow5\times 10^6\ g \end{gathered}$$ Recall that kilo- means $10^3$ so we make the $10^6$ into $10^3$, shifting the decimal point as necessary:
$$\begin{gathered} 5.0\times 10^6\ g\rightarrow5,000\times 10^3\ g \end{gathered}$$
We decreased the power of 10 by 3 so we MUST shift the decimal point to the right by 3 digits
Swap $10^3$ for kilo-: $$\begin{gathered} 5,000\times 10^3\ g\rightarrow5,000\ kg \end{gathered}$$ 2. Convert 3 mg to kg
Writing prefix as a power of 10: $$\begin{gathered} 3\ mg\rightarrow3\times 10^{-3}\ g \end{gathered}$$ Making $10^{-3}$ into $10^3$ since kilo- means $10^3$, shifting the decimal point as necessary:
$$\begin{gathered} 3\times10^{-3}\ g\rightarrow 0.000003 \times 10^3\ g \end{gathered}$$We increased the power of 10 by 6 so we MUST shift the decimal point to the left by 6 digits
Swap $10^3$ for kilo-: $$\begin{gathered} 0.000003\times 10^3\ g\rightarrow 0.000003\ kg \end{gathered}$$
Mission details
Convert the following:
- $13\ kg\ to\ mg$
- $20\ mg\ to\ kg$
- $2.47\ kg\ to\ Mg$
- $0.0037\ kg\ to\ mg$
- $1,200,000,000,000\ ng\ to\ kg$