A relation is a relationship between two sets. Relations can be:
- one-to-one e.g. each student in a class receiving one fruit
- one-to-many e.g. one drummer playing for many bands (he’s free this Saturday btw)
- many-to-one e.g. many persons following an artist (they all claim Kes is their husband)
- many-to-many e.g. citizens reading many newspapers to find a consensus on what is true
The set of all inputs (x values) is referred to as the domain. The set of all outputs (y values) is called the co-domain.
Functions
Functions are relationships between two sets (inputs and outputs) whereby each input has exactly one ($1$) corresponding output. A function can be taught of as a reliable ice-cream machine whereby inputting a certain ingredient will always produce the same result:
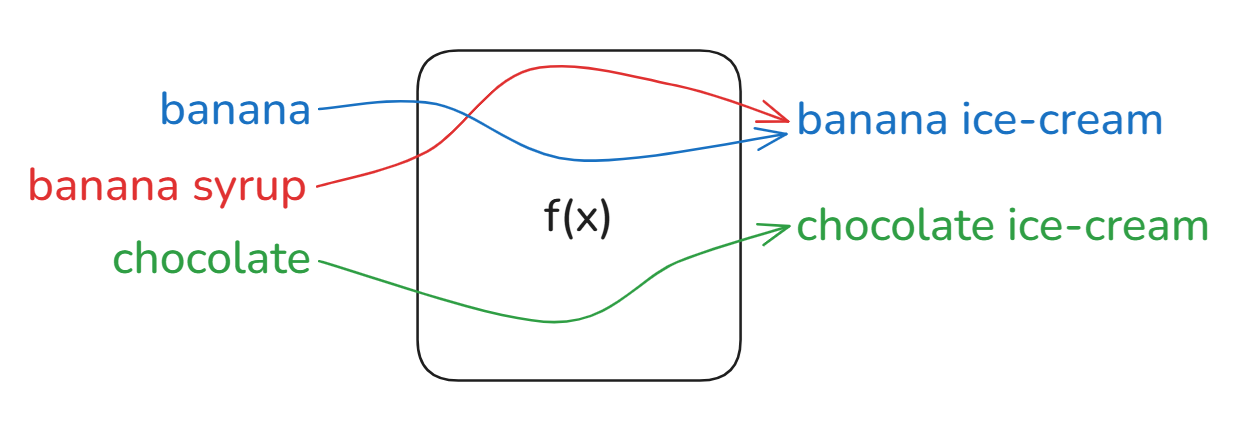
One input will never produce multiple outputs:
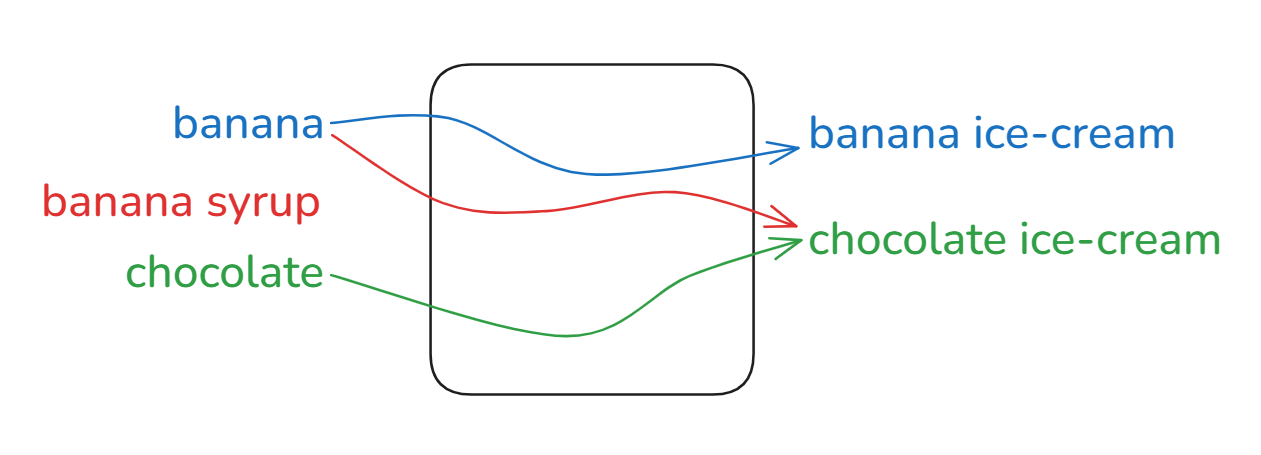
The machine above is unreliable because sometimes adding banana gives us banana ice-cream but other times adding banana gives us chocolate ice-cream. It would be better to have a machine that takes banana and produces chocolate ice-cream every time because at least we can depend/rely on it to produce the same output (chocolate ice-cream) every time for the same given input (banana).
Range
The range of a function is the set of the y values produced by the function.
All functions (reliable ice-cream machines) are relations (ice-cream machines) but not all relations (ice-cream machines) are functions (reliable ice-cream machines). Only one-to-one and many-to-one relations are functions.
The vertical line test
In this test, we simply draw a vertical line and if this line cuts the graph of the relation at more than one places, then we conclude that the relation is NOT a function.
Research Questions
Upon completion of this section you will be competent enough to answer the following:
- What is a relation?
- What is a function?
- Are all relations functions?
- Are all functions relations?
- What is meant by the domain?
- What is meant by the range?
- What do we use the vertical line test for?
- What is an injective (one-to-one) function?
- What is the algebraic method of determining if a function is injective?
- What is the horizontal line test used for?
- What is a surjective function?
- What is a bijective function?
- How do we find the inverse of a function?
- What is the geometric relationship of the inverse function to the original function?
- Can we find the inverse of a function which is not bijective?
- What relationship does the inverse of the inverse of a function have with the function itself?
- What is meant by the composition of two functions?
- Can you show that $ff^{-1}(x)=x$ and $f^{-1}f(x)=x$?
