Theory
Density($\rho$) is the mass ($m$) per unit volume ($V$) of a substance:
$$ \begin{equation}\begin{aligned} \rho=\frac{m}{V}\\ \end{aligned}\end{equation} $$The relative density is the ratio of the density of the substance to the density of a standard (usually water):
$$ \begin{equation}\begin{aligned} \rho_{rel}=\frac{\rho_{substance}}{\rho_{water}}\\ \end{aligned}\end{equation} $$The relative density of an irregular solid can thus be determined by finding the density of the solid and dividing it by the density of water. The relative density can also be found by taking the ratio of the masses of equal volumes of the solid and the water:
$$ \begin{equation}\begin{aligned} \rho_{rel}&=\frac{\rho_{substance}}{\rho_{water}}\times \frac{V}{V}\\ &=\frac{m_{substance}}{m_{water}}\\ \end{aligned}\end{equation} $$Aim
To determine the relative density of an irregular solid
Materials/Apparatus
- Eureka can
- Irregularly-shaped object
- Water
- Measuring cylinder
- Triple-beam balance of electronic balance
- Thin thread
Diagram
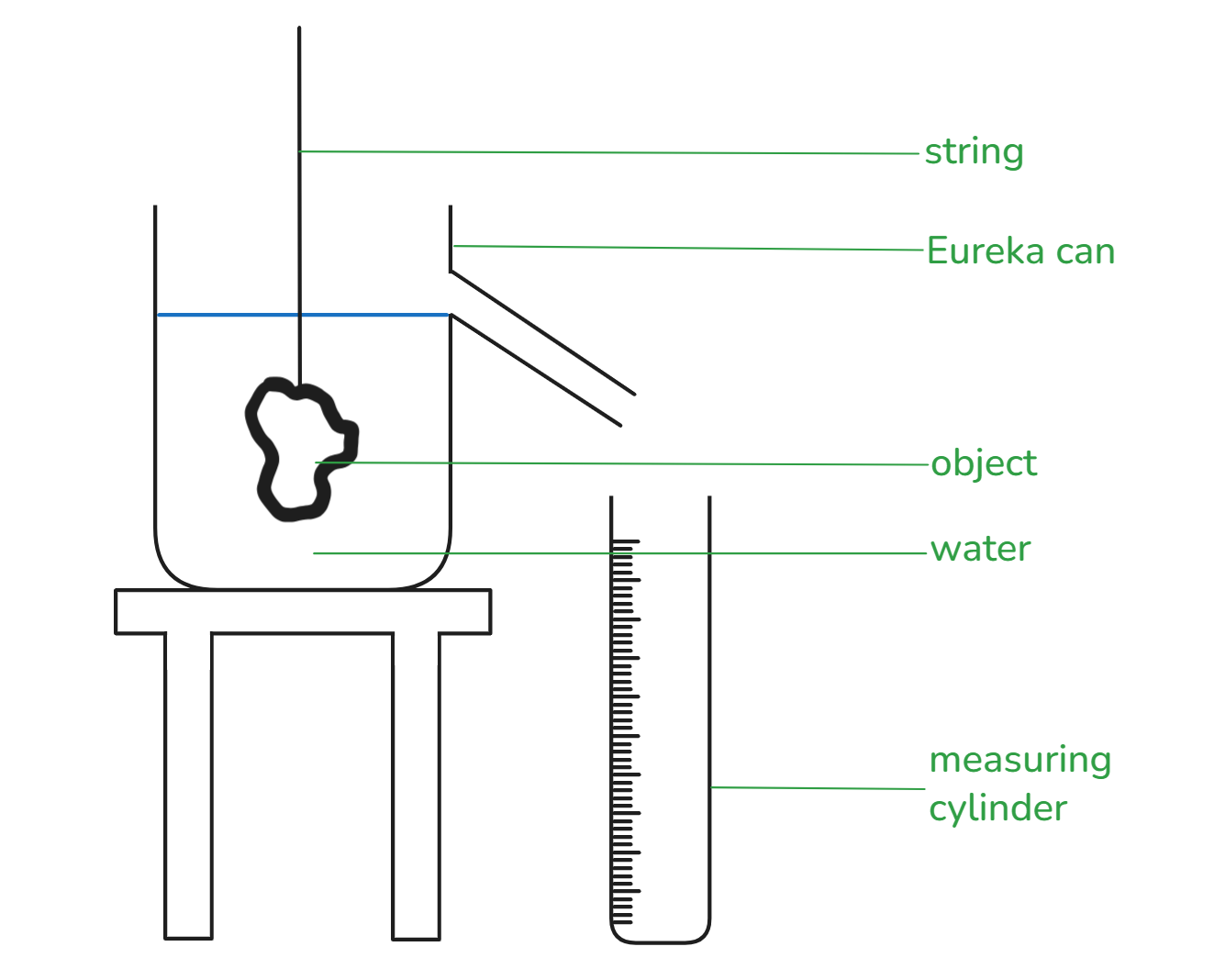
Method
- Measure the mass of the solid using the balance
- Fill the Eureka can with water and allow the excess water to flow out
- Measure the mass of the empty measuring cylinder
- Place the measuring cylinder under the spout of the Eureka can
- Suspend the object by using the thread and slowly lower it into the Eureka can until it is fully immersed in the water
- Measure the combined mass of the measuring cylinder and the water which overflows into the measuring cylinder
- Record the volume of water captured in the measuring cylinder
- Record the data in the table provided
Results
| Quantity | Value |
|---|---|
| Mass of solid ($g$) | |
| Mass of empty measuring cylinder ($g$) | |
| Combined mass of water and measuring cylinder ($g$) | |
| Volume of water captured in measuring cylinder ($cm^3$) |
Data Analysis
- Calculate the mass of the water captured in the measuring cylinder
- Calculate the density of the solid in $gcm^{-3}$
- Determine the relative density of the solid by using its density and the density of water
- Determine the relative density of the solid by using its mass and the mass of the equal volume of water captured in the measuring cylinder
- Are the two values for the relative density close to each other?
- List three ($3$) instances where deviations could have happened.
