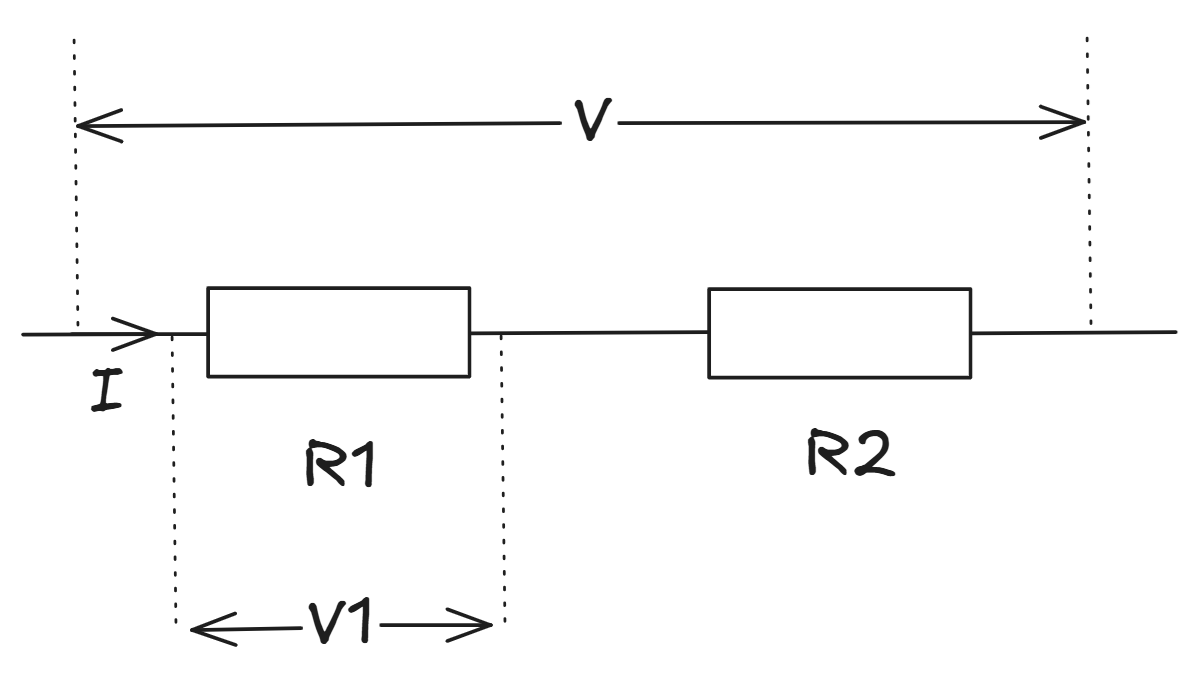
This device can split a larger potential, $V$ e.g. $9V$ into smaller, more useful potentials e.g. $1.5V$. Consider the two resistors, $R_1$ and $R_2$ in series with $V$ applied across them:
We know that due to conservation of charge, the same current flows through each of the resistors thus: $$ \begin{equation}\begin{aligned} I=\frac{V_1}{R_1}\\ I=\frac{V_2}{R_2}\\ \end{aligned}\end{equation} $$
That same current also flows through the combination of the two resistors, $R_T$: $$ \begin{equation}\begin{aligned} I=\frac{V}{R_T}\\ \end{aligned}\end{equation} $$
where, due to the resistors being in series: $$ \begin{equation}\begin{aligned} R_T=R_1+R_2\\ \end{aligned}\end{equation} $$
Thus we get: $$ \begin{equation}\begin{aligned} \frac{V_1}{R_1}&=\frac{V}{R_1+R_2}\\ \therefore V_1&=\frac{R_1}{R_1+R_2}V\\ \end{aligned}\end{equation} $$
The proportion of the voltages
The ratio of the target voltage, $V_1$ to the total voltage is the same as that of the target resistance, $R_1$ to the total resistance: $$ \begin{equation}\begin{aligned} \frac{V_1}{V}=&\frac{R_1}{R_T}\\ \text{OR }&\frac{R_1}{R_1+R_2}\\ \end{aligned}\end{equation} $$
Practice
- Find the possible output voltages across each resistor given that a voltage of $110V$ is applied across two resistors, $17\Omega$ and $22\Omega$, placed in series.
- Find the possible output voltages across each resistor given that a voltage of $110V$ is applied across three resistors, $17\Omega$, $22\Omega$ and $22\Omega$, placed in series.
- Given that an input voltage of $240V$ is placed across two resistors in series, one being $44\Omega$, find the resistance of the other resistor that will make the output voltage across the $44\Omega$ resistor $30V$.