Waves

A wave is a disturbance that transfers energy from one point to another, without the net displacement of matter. There are three ($3$) types of waves:

• Mechanical waves
• Electromagnetic waves
• Matter waves

Matter waves are associated with wave-particle duality. We know that light can sometimes behave as a wave and other times as a particle. By that logic, it is thus possible that other particles of matter can behave as waves.

Mechanical waves

These are waves that require the motion of particles in order to be propagated. There are two ($2$) types of mechanical waves:

• Transverse waves - in which the displacement of the particles is perpendicular to the direction of energy transfer e.g. water waves and light waves
• Longitudinal waves - in which the displacement of the particles is in the same direction as the direction of energy transfer e.g. sound waves

Because mechanical waves require the motion of particles, they cannot travel through a vacuum (the complete absence of matter).

Electromagnetic waves

These are light waves (both visible and invisible). They do not require the presence of matter in order to be propagated. Hence, they can travel through a vacuum e.g. light from the Sun travelling through space in order to reach the Earth. Although they can travel through space, they can also travel through matter e.g. light travelling through water, glass and air.

Terms associated with waves

Consider a wave with the following parts:

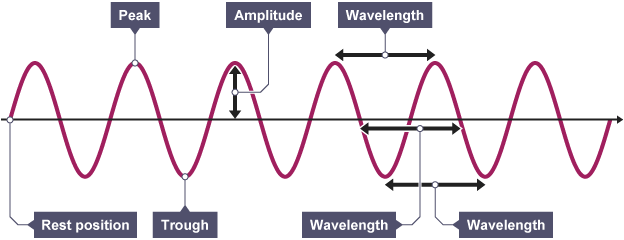
• Crest - the highest point on a wave
• Trough - the lowest point on a wave
• Wave front - the imaginary line/surface from which the wave originates. It is the rest position of the particles propagating the wave
• Amplitude - This is the maximum displacement of a particle from the wave front
• Wavelength ($\lambda$) - the distance between two successive crests or troughs or consecutive points on a wave
• Oscillation - this is the vibration motion as we move from one point of the wave to another
• Period ($T$) - this is the time taken to undergo one complete to-and-fro movement on the wave
• Frequency ($f$) - this is the number of oscillations completed per unit time. It is measured in Hertz ($Hz$)
• Speed - how fast a wave travels

Calculating speed of a wave

The speed of a wave is the product of its frequency and its wavelength:

$$ \begin{equation}\begin{aligned} v&=f\times \lambda\\ \end{aligned}\end{equation} $$

Because frequency is the reciprocal of period, we can have another variation of this formula: $$ \begin{equation}\begin{aligned} f&=\frac{1}{T}\\ \therefore v&=\frac{1}{T}\times \lambda\\ v&=\frac{\lambda}{T}\\ \end{aligned}\end{equation} $$

These formulae explain the relationship between speed and other variables but they do not consider the physical properties of the medium through which the wave is propagated. For a wave travelling through a string with tension, $\tau$ and linear mass density, $\mu$, the speed of the wave is given as $$ \begin{equation}\begin{aligned} v&=\sqrt{\frac{\tau}{\mu}}\\ \end{aligned}\end{equation} $$

Intensity

The intensity of a wave is the power transferred per unit area: $$ \begin{equation}\begin{aligned} I&=\frac{P}{A}\\ &\rightarrow \frac{W}{m^2}\\ &=Wm^{-2}\\ \end{aligned}\end{equation} $$

The SI unit is the Watt per square meter ($Wm^{-2}$).