We know that forces can cause changes in motion, size and shape. When we consider the shape/size changing aspect of forces, we are talking about deformation. Deformation is a change in the size or shape of a body or system e.g. stretching a rubber band, hitting a nail into a wooden board or having something hit your car and dent it.
Types of deformation
There are two ($2$) types of deformation:
- Elastic deformation - this is deformation whereby the object returns fully to its original shape after being deformed.
- Plastic deformation - this is deformation whereby the object does not return fully to its original shape after being deformed.
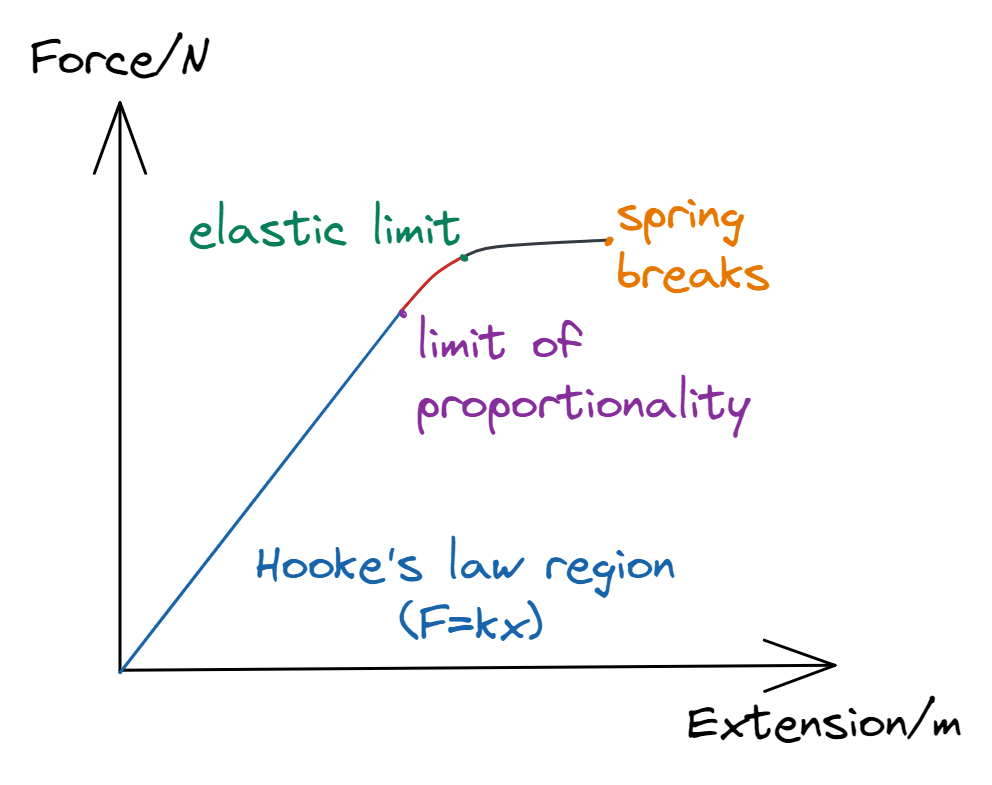
A material can experience both elastic and plastic deformation. It is just a matter of how much force is applied. Elastic deformation tends to happen on lower ranges of force. Eventually, if the force exceeds a certain value (called the elastic limit), plastic deformation takes over.
Hooke’s Law
The deformation on an object is directly proportional to the force applied to the object: $$ \begin{equation}\begin{aligned} F&=kx\\ \end{aligned}\end{equation} $$
where $k$ is the spring constant, usually measured in $Nm^{-1}$, for the given spring. There is a point called the limit of proportionality after which we do not use Hooke’s Law.
The deformation in the case of using a spring is called the extension. This is a change in length of the spring.
Example Determine the spring constant of a spring whose length is $4.5cm$ when no force is being applied and $5.7cm$ when a force of $3.2N$ is applied.
Solution The spring constant is $$ \begin{equation}\begin{aligned} k&=\frac{\Delta F}{\Delta x}\\ &=\frac{3.2N-0N}{0.057m-0.045m}\\ &=266.7Nm^{-1}\\ \end{aligned}\end{equation} $$
Potential energy stored in a spring
The elastic potential energy stored up in a spring is given by the formula $$ \begin{equation}\begin{aligned} E_P&=\frac{1}{2}kx^2\\ \end{aligned}\end{equation} $$
Force-extension graphs
This is a graph with extension plotted against force:
For the proportional section, before the limit of proportionality is exceeded, the gradient is the spring constant: $$ \begin{equation}\begin{aligned} m&=\frac{F}{x}\\ &=k\\ \end{aligned}\end{equation} $$
The area under a force extension graph is the work done in extending the spring.