Moments

The moment is the turning effect of a force. It is the product of the force ($F$) and the perpendicular distance between the pivot and the line of action of the force ($d$):

$$ \begin{equation}\begin{aligned} \text{moment} =F\times d\\ \end{aligned}\end{equation} $$

The SI unit of moments is thus: $$ \begin{equation}\begin{aligned} \text{moment} &=F\times d\\ &\rightarrow N\times m\\ &=Nm\\ \end{aligned}\end{equation} $$

The Principle of Moments

This states that, for a system in equilibrium, the sum of clockwise moments is equal to the sum of anti-clockwise moments.

$$ \begin{equation}\begin{aligned} \Sigma \text{anti-clockwise moments}&=\Sigma \text{clockwise moments}\\ F_1d_1&=F_2d_2\\ \end{aligned}\end{equation} $$

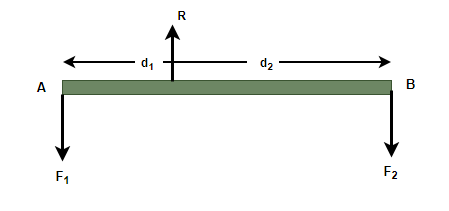
Example: Find the weight of a plus-sized child that will cause him/her to balance a seesaw if a child of weight $105N$ is sitting on the other side at a distance of $3m$ from the pivot. The plus-sized child is at a distance of $1.5m$ away from the pivot.

Solution: We have:

• $F_1=105N$
• $d_1=3m$
• $d_2=1.5m$

What we need to find:

• $F_2$

$$ \begin{equation}\begin{aligned} \Sigma \text{anti-clockwise moments}&=\Sigma \text{clockwise moments}\\ F_1d_1&=F_2d_2\\ 105N\times 3m&=F_2\times 1.5m\\ F_2&=\frac{105N\times 3m}{1.5m}\\ F_2&=210N\\ \end{aligned}\end{equation} $$

Example: Determine if the following system is in equilibrium:

• On one side, there is a $4N$ object at a distance of $5m$ away from the pivot
• On the other side, there are two objects, one of $7N$ at a distance of $1.3m$ and the other of $3N$ at a distance of $1.4m$ away from the pivot.

Solution: For a system in equilibrium: $$ \begin{equation}\begin{aligned} \Sigma \text{anti-clockwise moments}&=\Sigma \text{clockwise moments}\\ 4N\times 5m&=7N\times 1.3m+3N\times 1.4m\\ 20Nm&=9.1Nm+4.2Nm\\ 20Nm&\neq 13.3Nm\\ \end{aligned}\end{equation} $$

Because the sum of moments on each side are unequal, the system is not equilibrium by the principle of moments.

$$ \begin{equation}\begin{aligned} 1hp&=\frac{33,000(ft-lb)}{1 min}\\ 1hp&=\frac{torque\times RPM}{5252}\\ \end{aligned}\end{equation} $$

Couples

A couple is a pair of forces that only cause rotation. Recall that forces that cause translation and rotation. In order for a pair of forces to be considered as a couple, their translational effect must thus be zero. That is, they are equal and opposite.

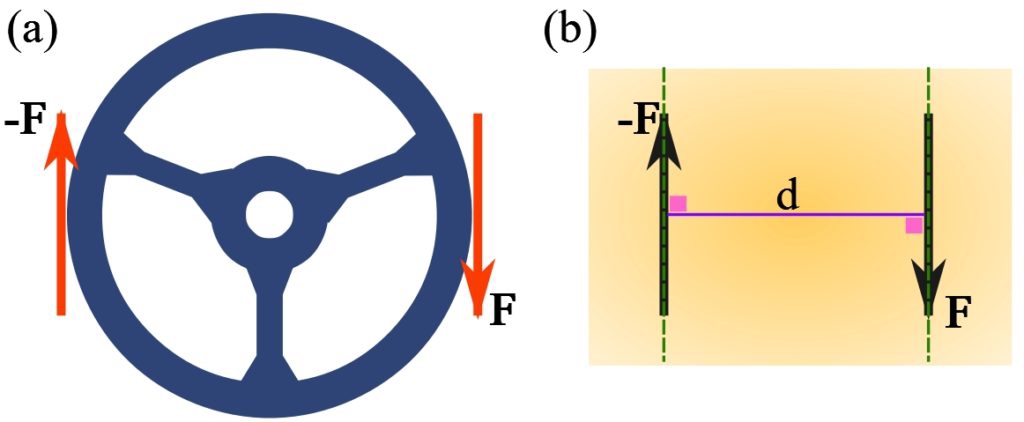
Consider the pair of forces applied to a steering wheel. If the forces are equal and opposite but do not have the same line of action, then the translation of the steering wheel will be zero ($0$) and the rotation will be significant.